The Figure Shows Three Forces Applied To A Trunk
News Leon
Mar 29, 2025 · 7 min read
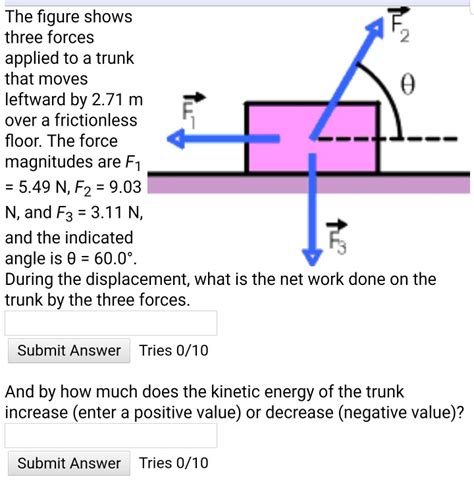
Table of Contents
Decoding the Forces: A Comprehensive Analysis of Three Forces Acting on a Trunk
The image depicting three forces applied to a trunk presents a classic problem in statics and dynamics. Understanding how these forces interact is crucial in numerous applications, from engineering design to everyday scenarios like moving furniture. This article delves deep into the physics behind this scenario, exploring various aspects such as equilibrium, resultant forces, moments, and the implications for the trunk's movement or stability. We’ll examine how different force combinations affect the trunk, considering various factors like friction and the trunk's center of gravity.
Understanding the Basics: Forces and Their Representation
Before diving into the specifics of the three forces acting on the trunk, let's refresh some fundamental concepts. A force is a vector quantity, meaning it possesses both magnitude (size) and direction. We typically represent forces using arrows: the arrow's length indicates the force's magnitude, and the arrow's direction indicates the force's direction of action. The point where the arrow originates represents the point of application of the force on the trunk.
Crucially, forces are interactive. Newton's Third Law of Motion states that for every action, there's an equal and opposite reaction. This means that if a force acts on the trunk, the trunk exerts an equal and opposite force on the object applying the force. We must consider all the forces acting on the trunk – including forces of reaction – for a complete analysis.
Analyzing the Three Forces: A Systematic Approach
Let's assume, for the sake of clarity, that the three forces acting on the trunk are labeled F1, F2, and F3. To analyze their combined effect, we need to consider several factors:
1. Magnitude and Direction of Each Force: The first step is to determine the magnitude (size) and direction of each force (F1, F2, and F3). This information is typically given in the problem statement or can be measured directly using appropriate tools. The units of force are usually Newtons (N). The direction can be specified using angles relative to a chosen coordinate system (e.g., the x-axis and y-axis).
2. Point of Application: Each force will have a specific point of application on the trunk. This is where the force is applied directly. The point of application plays a crucial role in determining the moment (torque) of the force, which we will discuss in detail later.
3. Resolving Forces into Components: To simplify calculations, it's often useful to resolve each force into its x and y components. This involves decomposing each force vector into its horizontal (x) and vertical (y) components using trigonometry. This allows for easier vector addition and analysis.
4. Vector Addition: Finding the Resultant Force: The combined effect of the three forces can be determined by finding the resultant force. This is done by vectorially adding F1, F2, and F3. There are several methods for this, including graphical methods (tip-to-tail method) and analytical methods (using vector components). The resultant force (FR) represents the net force acting on the trunk.
5. Equilibrium and Motion: If the resultant force (FR) is zero, the trunk is in static equilibrium. This means the trunk is either at rest or moving with a constant velocity. If FR is non-zero, the trunk will accelerate in the direction of FR. The magnitude of the acceleration is directly proportional to the magnitude of FR and inversely proportional to the mass of the trunk (Newton's Second Law: F = ma).
The Role of Moments (Torque): Rotation and Stability
Forces not only cause linear motion (translation) but also rotational motion. The tendency of a force to cause rotation is called moment or torque. The moment of a force is calculated as the product of the force's magnitude and the perpendicular distance from the force's line of action to the pivot point (or axis of rotation). This distance is often called the moment arm.
In the context of the trunk, the pivot point could be any point, but it's often convenient to choose the center of gravity of the trunk. The center of gravity is the point where the weight of the trunk can be considered to act. If the sum of the moments of all the forces acting on the trunk is zero, the trunk is in rotational equilibrium, meaning it's not rotating.
Determining the moments of F1, F2, and F3 about the trunk's center of gravity is crucial for determining its stability. If the net moment is non-zero, the trunk will rotate. The direction of rotation depends on the direction of the net moment: a clockwise net moment will cause clockwise rotation, and a counterclockwise net moment will cause counterclockwise rotation.
Friction: A Crucial Factor in Stability
Friction plays a vital role in the trunk's stability and motion. Friction is a force that opposes motion between two surfaces in contact. In this case, friction exists between the trunk and the surface it rests upon.
The maximum static friction force is proportional to the normal force (the force exerted by the surface on the trunk, perpendicular to the surface) and is determined by the coefficient of static friction (μs) between the trunk and the surface. Once the applied force exceeds the maximum static friction, the trunk will start moving, and the kinetic friction force (which is usually less than the static friction force) will then oppose the trunk's motion.
Considering friction is essential for a complete analysis of the three forces. If the horizontal component of the resultant force is less than the maximum static friction force, the trunk will remain stationary. If it exceeds the maximum static friction, the trunk will move.
Practical Applications and Real-World Scenarios
Understanding the interaction of multiple forces acting on an object like the trunk has wide-ranging applications across several fields:
- Engineering Design: Engineers use these principles to design structures, machines, and other systems that can withstand various forces and maintain stability.
- Robotics: Understanding forces and moments is crucial in robotics for precise manipulation and control of robotic arms and other mechanical systems.
- Construction: The principles of statics are essential in ensuring the stability and safety of buildings, bridges, and other structures.
- Everyday Life: Moving furniture, lifting heavy objects, and many other everyday tasks involve the application of forces and the need to understand equilibrium and stability.
Advanced Considerations: Beyond the Basics
The analysis can be extended to incorporate more complex factors:
- Multiple Dimensions: The problem can be extended to three dimensions, requiring more complex vector calculations and consideration of moments about multiple axes.
- Dynamic Analysis: Instead of static equilibrium, we might analyze the trunk's motion under the influence of the three forces, considering its acceleration and velocity over time.
- Non-rigid Bodies: If the trunk is not considered a rigid body (meaning it can deform), the analysis becomes more complex, requiring consideration of stress, strain, and material properties.
- External Factors: External factors such as wind resistance or other environmental forces might need to be included in a more comprehensive analysis.
Conclusion: The Importance of Force Analysis
Analyzing the forces acting on a trunk, seemingly a simple problem, reveals a rich tapestry of fundamental physics principles. Understanding how forces combine to produce resultant forces and moments, the role of friction, and the implications for equilibrium and motion are crucial in many fields, from engineering design to everyday activities. This comprehensive analysis provides a foundation for tackling more complex problems involving multiple forces and offers insight into the world of statics and dynamics. By systematically breaking down the problem and employing appropriate techniques, we can accurately predict and understand the behavior of the trunk under the influence of these three forces. Remember to always consider the context of the problem, the accuracy of measurements, and the various factors which may influence the outcome. This in-depth understanding equips individuals with the skills necessary to solve similar problems and confidently approach more complex scenarios.
Latest Posts
Latest Posts
-
One Billion Is How Many Crores
Apr 01, 2025
-
What Is The Oxidation State Of N In Nh4
Apr 01, 2025
-
Which Of The Following Compounds Is Are Chiral
Apr 01, 2025
-
48 As A Percentage Of 60
Apr 01, 2025
-
What Is The Oxidation Number Of Sulfur In Sulfuric Acid
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about The Figure Shows Three Forces Applied To A Trunk . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
