Sample Space For Tossing A Coin 3 Times
News Leon
Apr 02, 2025 · 6 min read
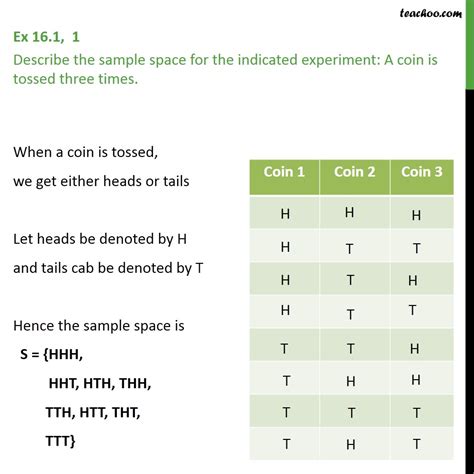
Table of Contents
Delving Deep into the Sample Space: Tossing a Coin Three Times
The seemingly simple act of tossing a coin three times opens a surprisingly rich landscape for exploring probability and statistics. While the individual outcomes might appear straightforward – heads or tails – the combined possibilities across three tosses reveal a complex sample space ripe for analysis. This article will delve into the intricacies of this sample space, exploring its construction, representation, and applications. We'll cover various methods of visualization and analysis, emphasizing the importance of understanding sample spaces in probability theory.
Understanding Sample Space
In probability theory, the sample space (often denoted as S or Ω) is the set of all possible outcomes of a random experiment. For our three-coin-toss experiment, each toss has two possible outcomes: heads (H) or tails (T). The sample space encompasses all possible sequences of these outcomes across the three tosses.
Constructing the Sample Space
To construct the sample space for tossing a fair coin three times, we can use a systematic approach. Let's represent heads as 'H' and tails as 'T'. The possible outcomes are:
- First Toss: H or T
- Second Toss: H or T
- Third Toss: H or T
Combining these possibilities, we can list all possible sequences:
- HHH
- HHT
- HTH
- HTT
- THH
- THT
- TTH
- TTT
This list represents the complete sample space, S, for our experiment. Therefore, S = {HHH, HHT, HTH, HTT, THH, THT, TTH, TTT}. The size of the sample space, denoted as |S|, is 8, indicating there are eight distinct possible outcomes.
Visualizing the Sample Space
Representing the sample space visually can significantly enhance understanding and analysis. Several methods are effective:
1. Tree Diagram
A tree diagram is a powerful visual tool for illustrating the sequential nature of the experiment. It begins with the first toss, branching into two possibilities (H or T). Each branch then further splits into two for the second toss, and so on. The final branches represent the complete set of possible outcomes. Creating a tree diagram allows for a clear visualization of how each outcome is generated.
(Insert a simple tree diagram here, showing the branching possibilities for each toss and the final eight outcomes)
2. Table Representation
A table can efficiently organize the sample space. We can use three columns, one for each toss, and list all possible combinations of H and T:
| Toss 1 | Toss 2 | Toss 3 | Outcome |
|---|---|---|---|
| H | H | H | HHH |
| H | H | T | HHT |
| H | T | H | HTH |
| H | T | T | HTT |
| T | H | H | THH |
| T | H | T | THT |
| T | T | H | TTH |
| T | T | T | TTT |
3. Venn Diagram (Less Suitable)
While Venn diagrams are excellent for visualizing relationships between sets, they are less suitable for this particular experiment because the outcomes are sequential and not easily represented as overlapping sets.
Analyzing the Sample Space: Probabilities and Events
Once we've established the sample space, we can analyze probabilities of specific events. An event is a subset of the sample space. For instance:
- Event A: Getting exactly two heads. This event includes the outcomes {HHT, HTH, THH}.
- Event B: Getting at least one tail. This event includes all outcomes except HHH: {HHT, HTH, HTT, THH, THT, TTH, TTT}.
- Event C: Getting all heads. This event includes only the outcome {HHH}.
Calculating the probability of an event involves dividing the number of favorable outcomes (outcomes within the event) by the total number of possible outcomes (the size of the sample space). Assuming a fair coin, each outcome in the sample space has an equal probability of 1/8.
- P(A) = P(exactly two heads) = 3/8 (three outcomes with exactly two heads)
- P(B) = P(at least one tail) = 7/8 (seven outcomes with at least one tail)
- P(C) = P(all heads) = 1/8 (one outcome with all heads)
Beyond Basic Probabilities: Exploring Combinations and Permutations
The three-coin-toss experiment provides a foundational example for understanding more complex probability concepts:
Combinations
Combinations are used when the order of outcomes doesn't matter. For example, if we only cared about the number of heads and tails, regardless of the order, we'd use combinations. In this case, there are four possible combinations:
- 3 heads, 0 tails
- 2 heads, 1 tail
- 1 head, 2 tails
- 0 heads, 3 tails
Permutations
Permutations are used when the order of outcomes matters. Our original sample space uses permutations because HHT is distinct from HTH, even though both have two heads and one tail. The number of permutations is calculated as n! / (n-r)!, where n is the number of trials (3 tosses) and r is the number of successes (e.g., number of heads).
Applications and Extensions
Understanding sample spaces extends far beyond simple coin tosses. The principles apply to various scenarios:
- Genetics: Predicting the probability of inheriting specific traits.
- Quality Control: Assessing the probability of defective items in a production batch.
- Medicine: Calculating the likelihood of disease transmission.
- Sports: Analyzing the probability of winning a game or tournament.
- Weather Forecasting: Determining the chance of rain or other weather conditions.
The concept of a sample space forms the bedrock for understanding conditional probability, Bayes' theorem, and many other advanced statistical concepts. The seemingly simple act of tossing three coins provides a powerful entry point into the fascinating world of probability and statistics.
Expanding the Experiment: More Coins or Different Probabilities
We can easily extend this analysis to more than three coin tosses. With four tosses, the sample space expands to 16 possibilities (2<sup>4</sup>). With n tosses, the sample space has 2<sup>n</sup> outcomes.
We can also explore scenarios with biased coins, where the probability of heads (p) is not equal to 0.5. In such cases, the probability of each outcome in the sample space will no longer be uniformly 1/8, but will depend on the value of p. For example, if p = 0.6 (a biased coin favoring heads), the probability of getting HHH would be (0.6)<sup>3</sup>, while the probability of getting TTT would be (0.4)<sup>3</sup>.
Conclusion: The Power of the Sample Space
The sample space, though seemingly a simple concept, is fundamental to probability theory. By systematically identifying and visualizing all possible outcomes, we build a solid foundation for analyzing probabilities, exploring events, and applying these principles to real-world situations. The three-coin-toss experiment, in its simplicity, demonstrates the power and versatility of the sample space concept and serves as an excellent starting point for delving into the broader world of probability and statistics. Understanding sample spaces is crucial for anyone seeking to grasp the fundamental principles of probability and their wide-ranging applications. From simple games of chance to complex scientific modeling, the systematic approach to defining and visualizing sample spaces remains an indispensable tool.
Latest Posts
Latest Posts
-
Why Are Fleas Hard To Squish
Apr 03, 2025
-
How Many Chromosomes In A Daughter Cell
Apr 03, 2025
-
Why Do Bones Heal Quicker Than Cartilage
Apr 03, 2025
-
Can Magnitude Be Negative In Physics
Apr 03, 2025
-
What Is The Area Of Triangle Rst
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Sample Space For Tossing A Coin 3 Times . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
