Lines Of Symmetry On An Octagon
News Leon
Mar 30, 2025 · 5 min read
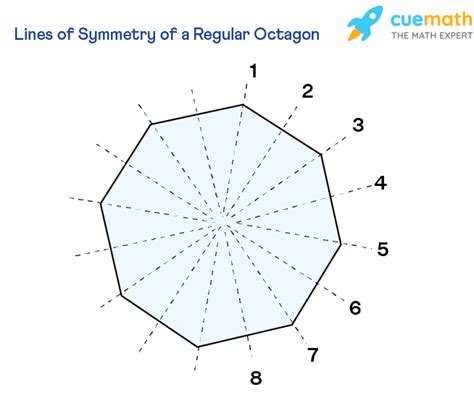
Table of Contents
Lines of Symmetry on an Octagon: A Comprehensive Guide
Symmetry, a concept fundamental to mathematics and art, finds a captivating expression in geometric shapes. Among these, the octagon, with its eight sides and angles, presents a fascinating study in lines of symmetry. This comprehensive guide delves into the intricacies of symmetry in octagons, exploring different types of symmetry, methods for identifying lines of symmetry, and practical applications of this geometrical concept.
Understanding Symmetry
Before we dive into the specifics of octagonal symmetry, let's establish a clear understanding of what symmetry means. In geometry, symmetry refers to a correspondence in size, form, or arrangement of parts on opposite sides of a plane, line, or point. This means that if you were to fold a symmetrical shape along a line, both halves would perfectly overlap. This line is known as a line of symmetry or axis of symmetry.
There are several types of symmetry, including:
- Reflectional symmetry (line symmetry): This is the most common type of symmetry, where a shape can be folded along a line, and the two halves mirror each other. This is the type of symmetry we'll be primarily focusing on with octagons.
- Rotational symmetry: This occurs when a shape can be rotated around a central point by a certain angle and still look the same. Octagons also exhibit rotational symmetry.
- Translational symmetry: This refers to a pattern that repeats itself along a line. Octagons, in their singular form, do not possess translational symmetry.
Lines of Symmetry in Regular Octagons
A regular octagon is defined as an octagon where all eight sides are of equal length, and all eight interior angles are equal (135° each). The symmetry of a regular octagon is particularly striking. Let's explore how to identify its lines of symmetry:
Identifying Lines of Symmetry
A regular octagon has a total of eight lines of symmetry. These lines can be categorized into two types:
1. Lines of symmetry connecting opposite vertices: There are four lines of symmetry that connect opposite vertices (corners) of the octagon. These lines pass directly through the center of the octagon, dividing it into two equal halves. Imagine drawing a line from one corner to the corner directly opposite it – that's a line of symmetry.
2. Lines of symmetry connecting midpoints of opposite sides: There are four additional lines of symmetry that connect the midpoints of opposite sides of the octagon. These lines also pass through the center, creating perfectly mirrored halves. Find the midpoint of one side, and draw a line to the midpoint of the opposite side – this is another line of symmetry.
Visualizing the Lines of Symmetry
To visualize these lines of symmetry, imagine an octagon drawn on a piece of paper. You can fold the paper along each of these eight lines, and the two halves will perfectly overlap, confirming their symmetrical nature. This is a hands-on way to understand the concept of line symmetry in a regular octagon.
Lines of Symmetry in Irregular Octagons
An irregular octagon is one where the sides and angles are not all equal. The number of lines of symmetry in an irregular octagon can vary greatly. It might have zero lines of symmetry, one line of symmetry, or even, in rare cases, more than one, but fewer than eight. Predicting the number of lines of symmetry without a visual representation is very difficult. Each case must be considered individually.
It's crucial to analyze the specific arrangement of sides and angles to determine the presence and number of lines of symmetry. There's no simple formula to predict the number of lines of symmetry for irregular octagons like there is for regular octagons. One must use visual inspection and potentially folding techniques (if the octagon is a physical shape) to identify any existing lines of symmetry.
Rotational Symmetry in Octagons
While our focus is on lines of symmetry, it's important to acknowledge the rotational symmetry present in octagons. A regular octagon has rotational symmetry of order 8. This means it can be rotated eight times (by 45° increments) around its center point and still look exactly the same. This rotational symmetry complements the reflectional symmetry discussed earlier, enriching the overall symmetry of the shape. Irregular octagons will have varying degrees of rotational symmetry or potentially none at all.
Applications of Octagonal Symmetry
The understanding of symmetry, especially in octagons, has far-reaching applications across various fields:
-
Architecture and Design: Octagons, with their inherent symmetry, are often employed in architectural designs for their aesthetic appeal and structural stability. Consider the many examples of octagonal buildings and designs you can observe. From ancient structures to modern designs, the aesthetic and structural strengths of an octagon are a driving force behind this design choice.
-
Art and Crafts: Artists and craftspeople utilize octagonal symmetry to create visually pleasing patterns and designs. The symmetrical nature of octagons facilitates the creation of balanced and harmonious compositions in various art forms, leading to visually stimulating works of art. This is evident across numerous cultures and artistic traditions.
-
Engineering and Technology: Octagonal shapes and their inherent symmetry find applications in engineering and technology, improving functionality and streamlining designs. This can range from machine parts with symmetrical designs to various patterns that benefit from the stability and efficiency that are afforded by this geometry.
-
Mathematics and Geometry: The study of symmetry in octagons and other geometric shapes contributes to the broader understanding of mathematical concepts and their interrelationships, further developing the foundational principles of geometry and mathematical applications.
Conclusion
Lines of symmetry in octagons, particularly regular octagons, present a fascinating area of study within geometry. The eight lines of symmetry, four connecting opposite vertices and four connecting midpoints of opposite sides, create a visually striking and mathematically precise structure. Understanding this symmetry has practical implications across various disciplines, showcasing the importance of geometric principles in our world. Whether you are an artist, architect, engineer, or math enthusiast, the exploration of octagonal symmetry offers a rewarding journey into the world of shapes and their captivating properties. The intricate interplay between reflectional and rotational symmetry in octagons highlights the elegant beauty and practical utility of this geometric figure. This detailed exploration provides a strong foundation for further investigations into the world of symmetry and its extensive applications. The mathematical elegance and visual appeal of the octagon make it a consistently inspiring topic within both artistic and scientific pursuits.
Latest Posts
Latest Posts
-
Which Of The Following Is Not A Lymphatic Organ
Apr 01, 2025
-
An Astronauts Weight On Earth Is 800 N
Apr 01, 2025
-
What Is The Percent Of 13 20
Apr 01, 2025
-
If A Transversal Intersects Two Parallel Lines Then
Apr 01, 2025
-
State Any Two Effects Of Force
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Lines Of Symmetry On An Octagon . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
