Is The Square Root Of 23 A Rational Number
News Leon
Mar 30, 2025 · 5 min read
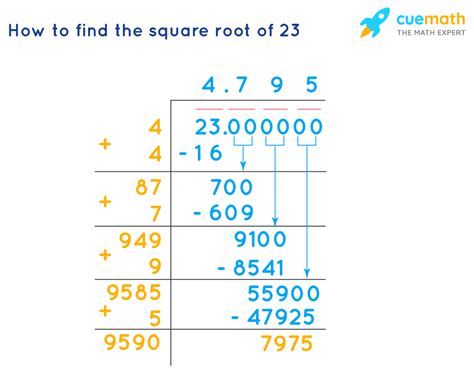
Table of Contents
Is the Square Root of 23 a Rational Number? A Deep Dive into Irrationality
The question of whether the square root of 23 is a rational number is a fundamental concept in mathematics, touching upon the core distinctions between rational and irrational numbers. Understanding this concept not only solidifies your grasp of number theory but also builds a strong foundation for more advanced mathematical explorations. Let's delve into this fascinating topic, exploring the definition of rational numbers, the properties of square roots, and the definitive proof regarding the square root of 23.
Understanding Rational Numbers
Before we tackle the square root of 23, it's crucial to define what a rational number actually is. A rational number is any number that can be expressed as a fraction p/q, where both 'p' and 'q' are integers (whole numbers), and 'q' is not equal to zero. This seemingly simple definition has profound implications for the entire number system. Examples of rational numbers include:
- 1/2: A simple fraction representing one-half.
- 3/4: Three-quarters.
- -5/7: A negative fraction.
- 2: This can be written as 2/1. All integers are rational numbers.
- 0.75: This can be expressed as the fraction 3/4. Terminating and repeating decimals are rational.
The key takeaway is that a rational number can always be expressed as a precise ratio of two integers.
Irrational Numbers: The Counterpoint to Rationality
Conversely, an irrational number cannot be expressed as a simple fraction of two integers. Their decimal representations are neither terminating (ending) nor repeating. Famous examples of irrational numbers include:
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159...
- e (Euler's number): The base of natural logarithms, approximately 2.71828...
- √2 (The square root of 2): This number, approximately 1.41421..., cannot be expressed as a fraction of two integers.
These numbers, while seemingly less "neat" than rational numbers, are equally important and fundamental in mathematics. They represent a vast and uncountable set of numbers filling the gaps between rational numbers on the number line.
Exploring Square Roots
A square root of a number 'x' is a number 'y' such that y² = x. For example, the square root of 9 is 3 because 3² = 9. However, not all square roots result in rational numbers. This is where the nature of the number inside the square root becomes crucial.
The Proof: Why √23 is Irrational
To prove that √23 is irrational, we'll employ a common proof technique used to demonstrate the irrationality of √2 and other similar numbers. This method relies on the concept of contradiction. We'll start by assuming the opposite of what we want to prove – that √23 is rational – and then show that this assumption leads to a logical contradiction.
1. Assumption: Let's assume, for the sake of contradiction, that √23 is a rational number. This means we can express it as a fraction p/q, where 'p' and 'q' are integers, 'q' is not zero, and the fraction is in its simplest form (meaning 'p' and 'q' have no common factors other than 1).
2. Squaring Both Sides: If √23 = p/q, then squaring both sides gives us: 23 = p²/q²
3. Rearranging the Equation: We can rearrange this equation to: 23q² = p²
4. Deduction about Divisibility: This equation tells us that p² is divisible by 23. Since 23 is a prime number, this implies that 'p' itself must also be divisible by 23. We can express this as p = 23k, where 'k' is an integer.
5. Substitution: Now, substitute p = 23k back into the equation 23q² = p²:
23q² = (23k)² 23q² = 529k²
6. Simplification: Divide both sides by 23:
q² = 23k²
7. The Contradiction: This equation shows that q² is also divisible by 23, and therefore 'q' must be divisible by 23.
This is where the contradiction arises. We initially assumed that p/q was in its simplest form, meaning 'p' and 'q' share no common factors other than 1. However, we've just shown that both 'p' and 'q' are divisible by 23. This is a contradiction, invalidating our initial assumption.
8. Conclusion: Since our assumption that √23 is rational leads to a contradiction, our initial assumption must be false. Therefore, √23 is an irrational number.
Implications and Further Exploration
The irrationality of √23, and indeed most square roots of non-perfect squares, highlights the richness and complexity of the number system. It underscores that the rational numbers, while dense on the number line, do not encompass all numbers. Irrational numbers are an integral part of the mathematical landscape, essential for many fields, including:
- Geometry: Calculations involving circles, triangles, and other shapes often involve irrational numbers like π and √2.
- Calculus: Limits, derivatives, and integrals often deal with irrational numbers in their calculations.
- Physics: Many physical constants and calculations utilize irrational numbers.
This exploration of √23 provides a clear and concise understanding of the difference between rational and irrational numbers. Understanding this distinction is fundamental for anyone seeking a deeper understanding of mathematics and its applications in various fields. The proof presented highlights the power of mathematical reasoning and the elegance of proof by contradiction. By understanding this proof, you not only learn about the specific case of √23 but also gain a broader appreciation for the rigorous logic that underpins mathematical truths. The exploration extends beyond this particular number, offering a pathway to explore other irrational numbers and the fascinating complexities of the number system as a whole. Further investigation could include examining the properties of other square roots, exploring transcendental numbers (a subset of irrational numbers), and delving into the fascinating history of the discovery and understanding of irrational numbers.
Latest Posts
Latest Posts
-
State Any Two Effects Of Force
Apr 01, 2025
-
How Many Electrons Does Sodium Have In Its Outer Shell
Apr 01, 2025
-
Dense Irregular Connective Tissue Will Be Found In The
Apr 01, 2025
-
Which Of The Following Organisms Can Fix Nitrogen
Apr 01, 2025
-
Which Of The Following Is Correct About Viruses
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Is The Square Root Of 23 A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
