Is The Following Relation A Function
News Leon
Mar 26, 2025 · 5 min read
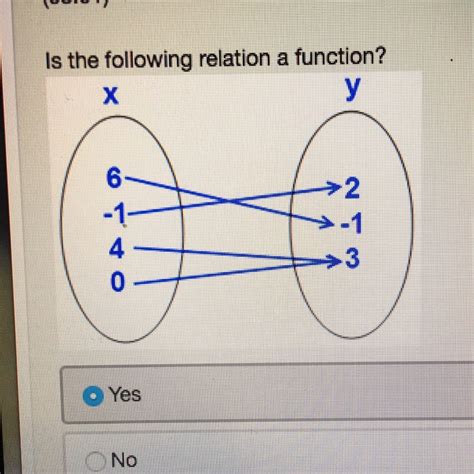
Table of Contents
- Is The Following Relation A Function
- Table of Contents
- Is the Following Relation a Function? A Comprehensive Guide
- Understanding the Definition of a Function
- Methods for Determining if a Relation is a Function
- 1. The Vertical Line Test (Graphical Method)
- 2. The Set of Ordered Pairs (Tabular Method)
- 3. The Equation Method (Algebraic Method)
- 4. Mapping Diagram Method
- Real-World Applications of Functions
- Advanced Concepts and Considerations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Is the Following Relation a Function? A Comprehensive Guide
Determining whether a relation is a function is a fundamental concept in mathematics, particularly in algebra and calculus. Understanding this distinction is crucial for progressing to more advanced topics. This comprehensive guide will delve into the definition of a function, explore various methods for identifying functions, and provide numerous examples and non-examples to solidify your understanding. We'll also touch upon the importance of this concept in real-world applications.
Understanding the Definition of a Function
A function is a special type of relation where each input value (often denoted as 'x' or the independent variable) corresponds to exactly one output value (often denoted as 'y' or the dependent variable). This is often expressed as a mapping from a set of inputs (the domain) to a set of outputs (the range). The key characteristic is the uniqueness of the output for every input. If a single input maps to multiple outputs, it's not a function.
Think of a function like a machine: you put an input into the machine, and it produces exactly one output. If the machine could produce multiple outputs for the same input, it wouldn't be a well-defined function.
Methods for Determining if a Relation is a Function
Several methods can be employed to determine whether a given relation represents a function:
1. The Vertical Line Test (Graphical Method)
This is a visual method applicable when the relation is represented graphically on a Cartesian plane. Draw vertical lines across the graph. If any vertical line intersects the graph at more than one point, the relation is not a function. If every vertical line intersects the graph at most once, the relation is a function. This test leverages the uniqueness requirement of function outputs.
Example: Consider the graph of a circle. A vertical line drawn through the circle will intersect it at two points in most places. Therefore, a circle is not a function.
Example: The graph of a straight line (except a vertical line) will always pass the vertical line test. Each x-value corresponds to only one y-value. Therefore, a straight line (excluding vertical lines) is a function.
2. The Set of Ordered Pairs (Tabular Method)
If the relation is given as a set of ordered pairs (x, y), examine the x-values. If any x-value appears more than once with different y-values, the relation is not a function. If each x-value is associated with only one y-value, the relation is a function.
Example: The set {(1, 2), (2, 3), (3, 4), (4, 5)} is a function because each x-value appears only once.
Example: The set {(1, 2), (1, 3), (2, 4)} is not a function because the x-value 1 is associated with two different y-values (2 and 3).
3. The Equation Method (Algebraic Method)
If the relation is defined by an equation, try to solve for y in terms of x. If you can obtain a unique solution for y for every x in the domain, the relation is a function. If you get multiple solutions for y for a single x, it's not a function.
Example: The equation y = x² is a function because for every value of x, there's only one corresponding value of y.
Example: The equation x = y² is not a function because for a positive x, there are two possible values of y (positive and negative square root of x).
4. Mapping Diagram Method
A mapping diagram visually represents the relation between inputs and outputs. Draw two sets, one for the domain (inputs) and one for the range (outputs). Draw arrows connecting each input to its corresponding output. If any input has more than one arrow pointing to different outputs, the relation is not a function.
Example: A mapping where 'a' maps to 1, 'b' maps to 2, and 'c' maps to 3 is a function.
Example: A mapping where 'a' maps to 1 and 'a' also maps to 2 is not a function because 'a' has two outputs.
Real-World Applications of Functions
The concept of functions is pervasive in various fields:
- Physics: Many physical laws are expressed as functions. For example, the distance traveled by a falling object is a function of time.
- Engineering: In designing structures or circuits, engineers use functions to model relationships between variables.
- Economics: Economic models often employ functions to describe supply and demand, cost and revenue.
- Computer Science: Functions are fundamental building blocks of programming languages. They encapsulate a specific task and return a value based on input.
- Biology: Population growth can be modeled using functions.
- Finance: Compound interest calculations involve functions relating principal, interest rate, and time.
Advanced Concepts and Considerations
-
Domain and Range: Understanding the domain (set of all possible input values) and range (set of all possible output values) is crucial for working with functions. Sometimes, restrictions are placed on the domain to ensure the function is well-defined (e.g., avoiding division by zero or taking the square root of a negative number).
-
Function Notation: The notation f(x) is commonly used to represent a function, where 'f' is the name of the function and 'x' is the input variable. f(x) denotes the output value of the function for a given input x.
-
Inverse Functions: An inverse function reverses the process of the original function. Not all functions have inverse functions; a function must be one-to-one (each output corresponds to a unique input) to have an inverse.
-
Composite Functions: A composite function is a function formed by applying one function to the result of another function. This is often denoted as (f ∘ g)(x) = f(g(x)).
Conclusion
Determining whether a relation is a function is a cornerstone of mathematical understanding. By mastering the different methods outlined – the vertical line test, the ordered pairs method, the equation method, and mapping diagrams – you can confidently analyze relations and identify functions. Remember that the key is the uniqueness of the output for each input. This seemingly simple concept has far-reaching applications across various disciplines, showcasing its fundamental importance in the broader world of mathematics and beyond. Practice with diverse examples to build your proficiency and deepen your understanding of this essential concept. The more you practice, the more intuitive the process will become.
Latest Posts
Latest Posts
-
Combine Terms 12a 26b 4b 16a
Mar 30, 2025
-
What Is The Difference Between Obligate And Facultative
Mar 30, 2025
-
What Is The Molecular Mass Of Ch3cooh
Mar 30, 2025
-
How Many Hours Is In 9 Days
Mar 30, 2025
-
The Si Unit Of Power Is
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Is The Following Relation A Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
