How Many Numbers Between 10 And 20 Are Perfect Squares
News Leon
Apr 06, 2025 · 4 min read
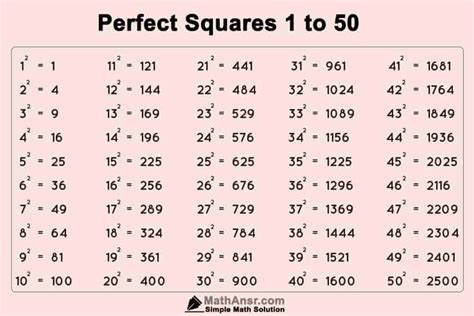
Table of Contents
How Many Numbers Between 10 and 20 Are Perfect Squares? A Deep Dive into Number Theory
The question, "How many numbers between 10 and 20 are perfect squares?" seems deceptively simple. However, exploring this seemingly straightforward query opens a door to a fascinating realm of mathematical concepts, including perfect squares, square roots, and the properties of integers. This article will not only answer the initial question but will also delve into the broader context of perfect squares, providing you with a solid understanding of the topic.
Understanding Perfect Squares
Before we tackle the specific range of numbers between 10 and 20, let's establish a clear understanding of what a perfect square actually is. A perfect square is a number that can be obtained by squaring (multiplying by itself) an integer. In simpler terms, it's the product of an integer multiplied by itself.
For example:
- 1 is a perfect square (1 x 1 = 1)
- 4 is a perfect square (2 x 2 = 4)
- 9 is a perfect square (3 x 3 = 9)
- 16 is a perfect square (4 x 4 = 16)
- 25 is a perfect square (5 x 5 = 25)
And so on. Notice a pattern? The perfect squares are always the result of squaring consecutive integers.
Identifying Perfect Squares: A Practical Approach
Identifying perfect squares often involves recognizing their unique characteristics. While calculating the square of each integer is feasible, especially for smaller numbers, there are alternative methods to quickly determine if a number is a perfect square.
One technique involves finding the square root of the number. If the square root is an integer, then the number is a perfect square. For example, the square root of 16 is 4 (an integer), confirming that 16 is a perfect square. However, the square root of 17 is approximately 4.123, which is not an integer; therefore, 17 is not a perfect square.
Another approach involves recognizing the patterns in the last digits of perfect squares. For instance, the last digit of a perfect square can only be 0, 1, 4, 5, 6, or 9. This observation can help eliminate certain numbers as potential perfect squares before you even calculate their square roots.
Answering the Question: Perfect Squares Between 10 and 20
Now, let's return to the original question: How many numbers between 10 and 20 are perfect squares?
Let's list the perfect squares:
- 1² = 1
- 2² = 4
- 3² = 9
- 4² = 16
- 5² = 25
Examining this list, we can see that only one number between 10 and 20 is a perfect square: 16.
Expanding the Scope: Exploring Perfect Squares in Larger Ranges
While the question focused on a relatively small range, understanding perfect squares within larger ranges is crucial for various mathematical applications. Let’s consider some broader explorations:
Perfect Squares in a Given Interval
To determine the number of perfect squares within a specific interval [a, b] (where a and b are integers), we can use the following approach:
- Find the square root of the lower bound (a): This gives you the smallest integer whose square is greater than or equal to a. Let's call this integer 'm'.
- Find the square root of the upper bound (b): This gives you the largest integer whose square is less than or equal to b. Let's call this integer 'n'.
- The number of perfect squares in the interval [a, b] is (n - m + 1): This formula accounts for all integers from m to n, inclusive.
For instance, if we want to find the number of perfect squares between 50 and 200, we would follow these steps:
- √50 ≈ 7.07. The smallest integer whose square is greater than or equal to 50 is 8. So, m = 8.
- √200 ≈ 14.14. The largest integer whose square is less than or equal to 200 is 14. So, n = 14.
- Number of perfect squares = (14 - 8 + 1) = 7. Therefore, there are 7 perfect squares between 50 and 200 (64, 81, 100, 121, 144, 169, 196).
Applications of Perfect Squares
The concept of perfect squares extends beyond simple number theory and has significant applications in various fields:
- Geometry: Calculating areas of squares, determining the length of the diagonal of a square using the Pythagorean theorem.
- Computer Science: Used in algorithms, particularly in tasks involving sorting and searching.
- Cryptography: Perfect squares play a role in cryptographic techniques, particularly in algorithms related to number theory.
- Physics: Certain physical phenomena are described using equations that involve perfect squares, for example, in calculations related to energy and motion.
Conclusion: Beyond the Simple Question
While the initial question, "How many numbers between 10 and 20 are perfect squares?", led us to the simple answer of one (16), exploring the underlying concepts of perfect squares provided a rich understanding of number theory and its applications. Understanding perfect squares isn't just about memorizing definitions; it's about recognizing patterns, applying logical reasoning, and appreciating the connections between seemingly simple mathematical concepts and their broader applications across various fields. This deeper dive underscores the beauty and utility of even the most elementary mathematical ideas. The exploration of perfect squares, as demonstrated here, offers a compelling example of how a simple question can trigger a much larger and more rewarding intellectual journey.
Latest Posts
Latest Posts
-
What Is The Double Coincidence Of Wants
Apr 07, 2025
-
Are Whole Numbers Closed Under Subtraction
Apr 07, 2025
-
Which Is Characteristic Of All Mixtures
Apr 07, 2025
-
How To Factor 2x 2 7x 3
Apr 07, 2025
-
2 3 3 Trimethylbut 1 Ene
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about How Many Numbers Between 10 And 20 Are Perfect Squares . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.