Greatest Common Factor Of 36 And 54
News Leon
Mar 21, 2025 · 5 min read
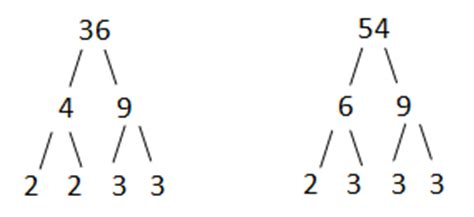
Table of Contents
Finding the Greatest Common Factor (GCF) of 36 and 54: A Comprehensive Guide
Finding the greatest common factor (GCF), also known as the greatest common divisor (GCD), of two numbers is a fundamental concept in mathematics with wide-ranging applications. This comprehensive guide will delve into the various methods for determining the GCF of 36 and 54, explaining the underlying principles and providing practical examples. We'll explore multiple approaches, ensuring a thorough understanding for both beginners and those looking to refresh their mathematical skills.
Understanding the Greatest Common Factor (GCF)
Before diving into the specific calculation for 36 and 54, let's solidify the definition of the GCF. The greatest common factor of two or more numbers is the largest number that divides evenly into all of them without leaving a remainder. It's essentially the largest shared factor among the numbers. Understanding this concept is crucial for simplifying fractions, solving algebraic equations, and many other mathematical operations.
Method 1: Prime Factorization
This method is considered the most fundamental and reliable way to find the GCF. It involves breaking down each number into its prime factors – numbers divisible only by 1 and themselves.
Step 1: Prime Factorization of 36
Let's start by finding the prime factorization of 36. We can use a factor tree:
36
/ \
2 18
/ \
2 9
/ \
3 3
Therefore, the prime factorization of 36 is 2 x 2 x 3 x 3, or 2² x 3².
Step 2: Prime Factorization of 54
Now, let's find the prime factorization of 54:
54
/ \
2 27
/ \
3 9
/ \
3 3
Therefore, the prime factorization of 54 is 2 x 3 x 3 x 3, or 2 x 3³.
Step 3: Identifying Common Factors
Compare the prime factorizations of 36 and 54:
- 36 = 2² x 3²
- 54 = 2 x 3³
We identify the common prime factors: both numbers share one factor of 2 and two factors of 3.
Step 4: Calculating the GCF
To find the GCF, we multiply the common prime factors together:
GCF(36, 54) = 2 x 3 x 3 = 18
Therefore, the greatest common factor of 36 and 54 is 18.
Method 2: Listing Factors
This method is more straightforward for smaller numbers but can become cumbersome for larger ones. It involves listing all the factors of each number and then identifying the largest common factor.
Step 1: Listing Factors of 36
The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36
Step 2: Listing Factors of 54
The factors of 54 are: 1, 2, 3, 6, 9, 18, 27, 54
Step 3: Identifying Common Factors
Now, compare the lists to find the common factors: 1, 2, 3, 6, 9, 18.
Step 4: Determining the GCF
The largest number in the list of common factors is 18. Therefore, the GCF(36, 54) = 18.
Method 3: Euclidean Algorithm
The Euclidean algorithm is a highly efficient method for finding the GCF, particularly useful for larger numbers. It's based on the principle that the GCF of two numbers doesn't change if the larger number is replaced by its difference with the smaller number. This process is repeated until the two numbers are equal, and that number is the GCF.
Step 1: Applying the Algorithm
Let's apply the Euclidean algorithm to 36 and 54:
- 54 = 1 x 36 + 18 (54 divided by 36 leaves a remainder of 18)
- 36 = 2 x 18 + 0 (36 divided by 18 leaves a remainder of 0)
Since the remainder is 0, the GCF is the last non-zero remainder, which is 18.
Therefore, GCF(36, 54) = 18.
Applications of the Greatest Common Factor
Understanding and calculating the GCF has numerous applications across various mathematical fields and real-world scenarios:
-
Simplifying Fractions: The GCF helps reduce fractions to their simplest form. For example, the fraction 36/54 can be simplified to 2/3 by dividing both the numerator and denominator by their GCF, which is 18.
-
Solving Algebraic Equations: Finding the GCF is crucial in factoring polynomials, a key step in solving many algebraic equations.
-
Geometry and Measurement: The GCF is useful in determining the dimensions of objects with specific constraints, such as finding the largest square tile that can perfectly cover a rectangular floor.
-
Number Theory: GCF plays a vital role in various number theory concepts, including modular arithmetic and cryptography.
-
Computer Science: Algorithms for finding the GCF are used in computer science for tasks such as data compression and encryption.
Beyond Two Numbers: Finding the GCF of Multiple Numbers
The methods described above can be extended to find the GCF of more than two numbers. For the prime factorization method, you would find the prime factorization of each number and then identify the common prime factors with the lowest exponent. For the Euclidean algorithm, you would apply it iteratively, finding the GCF of two numbers at a time, and then finding the GCF of the result and the next number, and so on.
For example, to find the GCF of 36, 54, and 72:
-
Prime Factorization:
- 36 = 2² x 3²
- 54 = 2 x 3³
- 72 = 2³ x 3²
The common prime factors are 2 and 3. The lowest exponent for 2 is 1, and the lowest exponent for 3 is 2. Therefore, GCF(36, 54, 72) = 2 x 3² = 18
-
Euclidean Algorithm (iterative):
- GCF(36, 54) = 18 (as calculated earlier)
- GCF(18, 72) = 18
Therefore, the GCF(36, 54, 72) = 18.
Conclusion
Finding the greatest common factor is a fundamental skill with broad applications in mathematics and beyond. This guide has demonstrated three effective methods – prime factorization, listing factors, and the Euclidean algorithm – for calculating the GCF, providing a comprehensive understanding of this crucial concept. Whether you are a student, a mathematician, or simply someone curious about numbers, mastering the calculation of the GCF will undoubtedly enhance your mathematical capabilities. Remember to choose the method best suited to the numbers involved; for larger numbers, the Euclidean algorithm proves to be the most efficient approach. Understanding the GCF provides a solid foundation for tackling more complex mathematical problems and applications.
Latest Posts
Latest Posts
-
Is Steel An Element Compound Or Mixture
Mar 28, 2025
-
Which Is Not A Function Of The Respiratory System
Mar 28, 2025
-
Seven More Than Twice A Number Is Equal To 25
Mar 28, 2025
-
The Part Of Earth Where Life Exists
Mar 28, 2025
-
What Intermolecular Forces Are Present In Ch4
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Greatest Common Factor Of 36 And 54 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
