Find The Volume Of Right Circular Cone
News Leon
Mar 31, 2025 · 5 min read
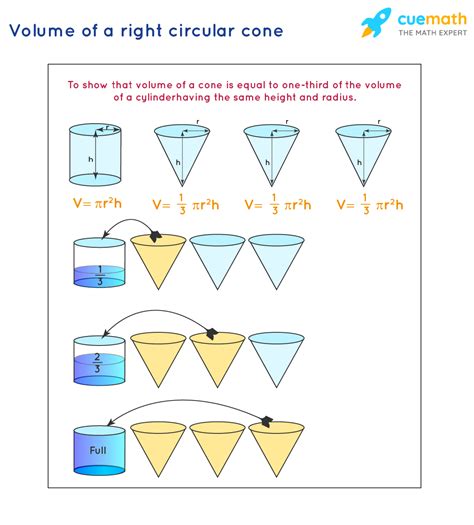
Table of Contents
Finding the Volume of a Right Circular Cone: A Comprehensive Guide
The right circular cone, a three-dimensional geometric shape, holds significant importance in various fields, from engineering and architecture to mathematics and computer graphics. Understanding how to calculate its volume is crucial for numerous applications. This comprehensive guide will delve into the intricacies of finding the volume of a right circular cone, covering the formula, its derivation, practical applications, and solving various related problems.
Understanding the Right Circular Cone
Before diving into the volume calculation, let's establish a clear understanding of what a right circular cone is. A right circular cone is a three-dimensional shape formed by connecting a circular base to a single point called the apex or vertex. The line segment connecting the apex to the center of the base is perpendicular to the base, forming a right angle. Key features include:
- Base: A circle at the bottom of the cone.
- Apex (Vertex): The pointed top of the cone.
- Height (h): The perpendicular distance from the apex to the center of the base.
- Radius (r): The radius of the circular base.
- Slant Height (l): The distance from the apex to any point on the circumference of the base. This is related to the radius and height by the Pythagorean theorem: l² = r² + h².
The Formula for the Volume of a Right Circular Cone
The formula for the volume (V) of a right circular cone is:
V = (1/3)πr²h
Where:
- V represents the volume of the cone.
- π (pi) is a mathematical constant, approximately equal to 3.14159.
- r represents the radius of the base.
- h represents the height of the cone.
Deriving the Formula: A Visual and Intuitive Approach
The formula isn't arbitrary; it's derived from the volume of a cylinder. Imagine a cylinder with the same base radius (r) and height (h) as the cone. The volume of a cylinder is given by: V<sub>cylinder</sub> = πr²h.
Now, consider filling the cone with sand or water. If you were to pour the contents of the filled cone into the cylinder, you'd find that it takes exactly three cone-fulls to completely fill the cylinder. This demonstrates that the volume of the cone is one-third the volume of a cylinder with the same base and height, leading directly to the cone volume formula: V<sub>cone</sub> = (1/3)πr²h.
This visual demonstration provides an intuitive understanding of why the (1/3) factor is present in the formula. A more rigorous mathematical derivation involves using calculus and integration, but this visual explanation offers a simpler, more accessible understanding for those without a calculus background.
Solving Problems: Practical Applications and Examples
Let's explore various examples to solidify our understanding of the formula and its application:
Example 1: A Simple Cone
A right circular cone has a radius of 5 cm and a height of 12 cm. Find its volume.
Solution:
- Identify the values: r = 5 cm, h = 12 cm.
- Apply the formula: V = (1/3)πr²h = (1/3)π(5 cm)²(12 cm) = (1/3)π(25 cm²)(12 cm) = 100π cm³
- Approximate the value: Using π ≈ 3.14159, V ≈ 314.16 cm³
Therefore, the volume of the cone is approximately 314.16 cubic centimeters.
Example 2: Finding the Radius
A cone has a volume of 150 cubic meters and a height of 10 meters. What is its radius?
Solution:
- Rearrange the formula to solve for r: r = √[(3V)/(πh)]
- Substitute the given values: r = √[(3 * 150 m³)/(π * 10 m)]
- Calculate: r ≈ √[14.32] ≈ 3.78 meters.
The radius of the cone is approximately 3.78 meters.
Example 3: Finding the Height
A cone has a volume of 200π cubic inches and a radius of 5 inches. Find its height.
Solution:
- Rearrange the formula to solve for h: h = (3V)/(πr²)
- Substitute the given values: h = (3 * 200π in³)/(π * (5 in)²)
- Calculate: h = 24 inches.
The height of the cone is 24 inches.
Advanced Applications and Considerations
The volume of a right circular cone is fundamental in various advanced applications:
- Civil Engineering: Calculating the volume of earth removed during excavation or the amount of concrete needed for a conical structure.
- Architecture: Designing structures with conical elements, like roofs or towers, requiring accurate volume calculations for material estimations.
- Manufacturing: Determining the capacity of conical containers or the amount of material required for manufacturing conical parts.
- Fluid Dynamics: Analyzing the flow of fluids in conical vessels or pipes.
- Calculus: The formula serves as a building block for more complex volume calculations using integration techniques for shapes that aren't perfectly conical.
Troubleshooting Common Mistakes
Several common mistakes can occur when calculating the volume of a right circular cone:
- Forgetting the (1/3) factor: This is the most common error. Always remember that the cone's volume is one-third the volume of the cylinder with the same base and height.
- Incorrect unit conversions: Ensure all measurements (radius and height) are in the same units before applying the formula. Convert all units to a consistent system (e.g., centimeters, meters, inches) to avoid errors.
- Misinterpreting the formula: Carefully substitute the correct values for radius and height into the formula.
- Approximating π inappropriately: While using 3.14 is often sufficient, for more precise calculations, use a more accurate approximation of π (e.g., 3.14159 or the π button on your calculator).
Conclusion: Mastering Cone Volume Calculations
Mastering the calculation of a right circular cone's volume is essential for anyone working with three-dimensional geometry. This guide has provided a comprehensive overview, covering the formula, its derivation, practical examples, and troubleshooting common errors. By understanding the underlying principles and practicing with various problems, you can confidently apply this knowledge across various disciplines and solve real-world problems involving conical shapes. Remember to always double-check your work, paying close attention to units and the (1/3) factor to achieve accurate and reliable results.
Latest Posts
Latest Posts
-
Ba No3 2 Na2so4 Balanced Equation
Apr 02, 2025
-
Which Phase Of Meiosis Separates Homologous Chromosomes
Apr 02, 2025
-
When Both Demand And Supply Change
Apr 02, 2025
-
Which Of The Following Statements Most Correctly Defines Homeostasis
Apr 02, 2025
-
Which Of The Following Is A Correct Match
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Find The Volume Of Right Circular Cone . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
