Find The Unknown Length X In The Following Figure
News Leon
Mar 29, 2025 · 6 min read
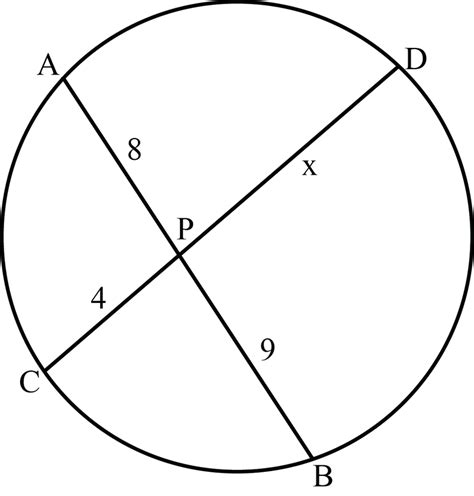
Table of Contents
Find the Unknown Length x: A Comprehensive Guide to Solving Geometric Problems
Finding an unknown length, often represented by 'x', within a geometric figure is a fundamental skill in mathematics. This seemingly simple task encompasses a wide range of problem-solving techniques, drawing upon various geometric theorems and principles. This comprehensive guide will equip you with the knowledge and strategies to tackle these problems confidently, regardless of the complexity of the figure. We'll explore different scenarios, from simple triangles to more complex polygons and combined shapes, illustrating each with clear examples and step-by-step solutions.
Understanding the Fundamentals: Key Geometric Theorems and Concepts
Before diving into specific problems, it's crucial to review some core geometric concepts and theorems that are essential for solving for 'x'. These form the bedrock upon which we'll build our problem-solving skills.
1. Pythagorean Theorem: The Cornerstone of Right-Angled Triangles
The Pythagorean theorem is arguably the most important theorem in right-angled triangle geometry. It states that in a right-angled triangle, the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides (the legs or cathetus). Mathematically:
a² + b² = c²
Where:
- 'a' and 'b' are the lengths of the legs.
- 'c' is the length of the hypotenuse.
This theorem is invaluable when 'x' represents the length of a side in a right-angled triangle, given the lengths of the other two sides.
2. Similar Triangles: Proportions and Ratios
Similar triangles are triangles that have the same shape but different sizes. Their corresponding angles are equal, and their corresponding sides are proportional. This proportionality is crucial for finding unknown lengths. If two triangles are similar, the ratio of their corresponding sides is constant. This allows us to set up proportions to solve for 'x'.
3. Trigonometric Ratios: Solving for Sides and Angles
Trigonometric ratios (sine, cosine, and tangent) provide a powerful tool for solving problems involving right-angled triangles, especially when we know one angle and one side. These ratios relate the angles of a right-angled triangle to the lengths of its sides:
- sin θ = opposite/hypotenuse
- cos θ = adjacent/hypotenuse
- tan θ = opposite/adjacent
Where θ represents the angle.
4. Area Formulas: Indirect Approaches to Finding 'x'
Sometimes, the area of a figure can provide indirect information that helps us find 'x'. For example, if we know the area of a triangle and the length of one side, we can use the area formula (Area = 1/2 * base * height) to solve for the height, which might be represented by 'x'. Similarly, knowing the area of a rectangle or other polygon can provide valuable constraints to help us find 'x'.
5. Properties of Isosceles and Equilateral Triangles: Exploiting Symmetry
Isosceles triangles have two equal sides, and equilateral triangles have all three sides equal. These properties significantly simplify calculations when dealing with such triangles. Knowing that two sides are equal can directly lead to finding 'x' if one of those sides is unknown.
Solving for 'x': Practical Examples and Step-by-Step Solutions
Let's delve into practical examples demonstrating how to find the unknown length 'x' in various geometric figures.
Example 1: Right-Angled Triangle
Imagine a right-angled triangle with legs of length 3 cm and 4 cm. Find the length of the hypotenuse (x).
Solution:
We can directly apply the Pythagorean theorem:
a² + b² = x²
3² + 4² = x²
9 + 16 = x²
25 = x²
x = √25 = 5 cm
Therefore, the length of the hypotenuse is 5 cm.
Example 2: Similar Triangles
Consider two similar triangles. The smaller triangle has sides of length 2 cm, 3 cm, and 4 cm. The larger triangle has sides of length 4 cm, 6 cm, and x cm. Find the value of x.
Solution:
Since the triangles are similar, the ratio of their corresponding sides is constant. We can set up a proportion:
2/4 = 4/x
Cross-multiplying gives:
2x = 16
x = 8 cm
Therefore, the unknown side of the larger triangle is 8 cm.
Example 3: Using Trigonometric Ratios
A right-angled triangle has an angle of 30 degrees and a hypotenuse of 10 cm. Find the length of the side opposite the 30-degree angle (x).
Solution:
We use the sine ratio:
sin 30° = opposite/hypotenuse
sin 30° = x/10
x = 10 * sin 30°
Since sin 30° = 0.5, we have:
x = 10 * 0.5 = 5 cm
Therefore, the length of the opposite side is 5 cm.
Example 4: Area and Unknown Length
A triangle has an area of 24 cm² and a base of 6 cm. Find the height (x) of the triangle.
Solution:
Using the area formula for a triangle:
Area = 1/2 * base * height
24 = 1/2 * 6 * x
24 = 3x
x = 8 cm
Therefore, the height of the triangle is 8 cm.
Example 5: Complex Shapes - Combining Techniques
Consider a figure composed of a rectangle and a right-angled triangle. The rectangle has a length of 8 cm and a width of 6 cm. The triangle sits atop the rectangle, sharing a side of length 8 cm with the rectangle. The hypotenuse of the triangle is x cm, and the other leg of the triangle is 4 cm. Find x.
Solution: This problem requires combining multiple techniques. First, we can solve for the height of the triangle using the Pythagorean Theorem:
height² + 8² = x²
height² + 64 = x²
Then we need additional information. The problem needs further definition to be solvable. We would need more information about the overall figure to definitively solve for 'x'. For instance, the overall height of the combined shape, or the angle of the triangle.
Advanced Techniques and Problem-Solving Strategies
For more complex geometric figures, more sophisticated techniques might be required:
- Coordinate Geometry: Representing shapes on a coordinate plane allows us to use algebraic methods to find unknown lengths.
- Vectors: Vector methods can be particularly useful for solving problems involving more complex shapes and relationships between lines and points.
- Calculus: In some advanced cases, calculus may be needed to determine lengths involving curves or other non-linear shapes.
Conclusion: Mastering the Art of Finding 'x'
Finding an unknown length 'x' in a geometric figure is a fundamental skill that can be mastered with practice and a solid understanding of the underlying geometric principles. By systematically applying the theorems and techniques outlined in this guide, you'll develop the confidence and capability to tackle a wide range of problems, from simple right-angled triangles to more complex shapes and scenarios. Remember, the key is to carefully analyze the figure, identify the relevant theorems or principles, and systematically work through the calculations. With practice, you'll develop an intuitive sense of how to approach these problems and find the solutions efficiently and effectively. Don't hesitate to revisit the fundamental concepts and practice regularly to further strengthen your skills in solving for 'x' and expanding your overall understanding of geometry.
Latest Posts
Latest Posts
-
What Is The Reciprocal Of 1 6
Mar 31, 2025
-
What Mineral Is The Hardest Known Substance In Nature
Mar 31, 2025
-
Which Organelle Is Enclosed By A Double Membrane
Mar 31, 2025
-
Compare And Contrast An Ecosystem And A Habitat
Mar 31, 2025
-
Network Layer Firewall Works As A
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Find The Unknown Length X In The Following Figure . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
