Electric Field Of A Cylindrical Shell
News Leon
Apr 06, 2025 · 6 min read
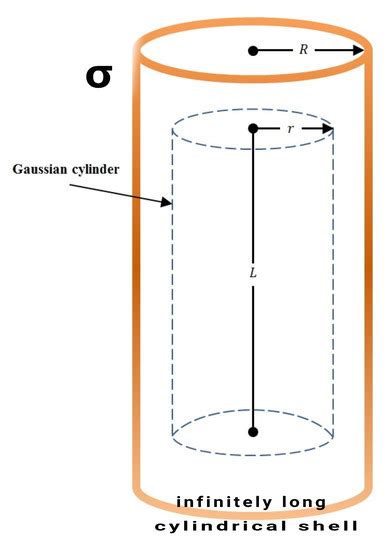
Table of Contents
Electric Field of a Cylindrical Shell: A Comprehensive Guide
The electric field generated by a cylindrical shell, whether charged uniformly or with a non-uniform charge distribution, is a classic problem in electrostatics with significant applications in various fields, from capacitor design to particle accelerators. Understanding this field requires a solid grasp of Gauss's law and its application to cylindrical symmetry. This article will provide a detailed exploration of the electric field of a cylindrical shell, covering both theoretical derivations and practical implications.
Understanding the Problem: Cylindrical Symmetry and Gauss's Law
Before delving into the specifics, it's crucial to establish a clear understanding of the problem's inherent symmetry. We're dealing with a cylindrical shell, meaning a hollow cylinder with a specific radius and height. The charge distribution on the shell will determine the complexity of the solution. For simplicity, we'll initially focus on a uniformly charged cylindrical shell.
Gauss's law is the cornerstone of solving this problem. It states that the net electric flux through any closed surface is proportional to the enclosed charge:
∮ E • dA = Q<sub>enc</sub> / ε₀
where:
- E is the electric field vector
- dA is a differential area vector
- Q<sub>enc</sub> is the enclosed charge
- ε₀ is the permittivity of free space
The key to applying Gauss's law effectively is choosing a suitable Gaussian surface – a closed surface that takes advantage of the symmetry of the problem. For a cylindrical shell, the ideal Gaussian surface is a cylinder coaxial with the charged shell. This choice simplifies the integral significantly because the electric field will be perpendicular to the curved surface of the Gaussian cylinder, and parallel to the flat ends.
Electric Field Inside a Uniformly Charged Cylindrical Shell
Let's consider the electric field inside a uniformly charged cylindrical shell with radius R and linear charge density λ (charge per unit length). Our Gaussian cylinder has a radius r < R and height h. Since no charge is enclosed within this Gaussian surface (Q<sub>enc</sub> = 0), Gauss's law immediately tells us:
∮ E • dA = 0
This implies that the electric field inside the cylindrical shell is zero. This is a significant result and a direct consequence of the symmetry and charge distribution. The electric fields produced by all parts of the shell cancel each other out at any point inside.
Practical Implications of Zero Electric Field Inside:
- Shielding: A cylindrical shell can be used as a shield against external electric fields. Any charges placed inside the shell will not be affected by external fields. This principle is fundamental in many electronic applications where sensitive components need protection.
- Capacitor Design: The zero internal field property has implications for capacitor design. The electric field primarily resides between the conductive plates, improving efficiency.
Electric Field Outside a Uniformly Charged Cylindrical Shell
Now let's consider the electric field outside the uniformly charged cylindrical shell (r > R). Our Gaussian cylinder still has radius r and height h. The enclosed charge is now the total charge on the section of the cylindrical shell within our Gaussian surface: Q<sub>enc</sub> = λh.
Applying Gauss's law:
∮ E • dA = (λh) / ε₀
Due to the symmetry, the electric field is constant in magnitude and radial. The flux through the flat ends of the Gaussian cylinder is zero, as the electric field is parallel to these surfaces. The flux through the curved surface is:
E * 2πrh = (λh) / ε₀
Solving for the electric field magnitude E:
E = λ / (2πε₀r)
This shows that the electric field outside a uniformly charged cylindrical shell decreases inversely with distance from the shell's axis. This is similar to the electric field of an infinitely long line of charge.
Practical Implications of External Electric Field:
- Electrostatic Interactions: This formula helps calculate the forces between charged particles near the cylinder, useful in particle physics experiments.
- Electrostatic Precipitation: The electric field outside the cylinder can be used to attract and collect charged particles, a principle applied in electrostatic precipitators to remove pollutants from industrial emissions.
Non-Uniform Charge Distributions: Complicating the Calculation
The previous sections addressed a uniform charge distribution. However, real-world scenarios often involve non-uniform charge distributions. This significantly complicates the calculation because the symmetry is broken. Gauss's law still applies, but the integral becomes far more challenging.
For non-uniform charge distributions, the surface charge density σ (charge per unit area) will be a function of the position on the shell's surface: σ = σ(θ, z), where θ is the azimuthal angle and z is the height along the cylinder. To calculate the electric field, one might need to use numerical methods or advanced integration techniques. The problem often breaks down into solving for infinitesimal charge elements and integrating their contributions to the electric field vector at a specific point.
Specific methods used for non-uniform charge distributions might include:
- Numerical Integration: Discretizing the cylindrical shell into small segments, calculating the field contribution from each segment, and summing the contributions. Methods like Monte Carlo integration might be employed.
- Series Expansion: For specific forms of non-uniform charge distributions, the electric field might be representable as a series expansion (e.g., Fourier series).
- Finite Element Method (FEM): A powerful computational technique often used for complex geometries and charge distributions.
Applications of Cylindrical Shell Electric Fields
The understanding of electric fields around cylindrical shells has numerous applications across various fields:
- Capacitors: Cylindrical capacitors utilize the principle of electric fields between concentric cylinders to store electrical energy. The capacitance of a cylindrical capacitor can be directly derived using the electric field expressions.
- Coaxial Cables: Coaxial cables utilize a central conductor surrounded by a cylindrical shield to transmit signals efficiently while minimizing interference. The electric field distribution plays a crucial role in signal integrity.
- Particle Accelerators: Cylindrical geometries are often used in particle accelerators to focus and guide charged particles. The electric fields influence the trajectory and energy of the particles.
- Electrostatic Precipitation: As mentioned previously, this technique utilizes the electric field around charged cylindrical structures to remove pollutants from air or gas streams.
- Medical Imaging: Certain medical imaging techniques rely on the interaction of electric fields with biological tissues. Understanding cylindrical field distributions can contribute to modeling these interactions.
Conclusion: A Fundamental Concept in Electrostatics
The electric field of a cylindrical shell, whether uniformly or non-uniformly charged, is a fundamental concept in electrostatics with far-reaching implications. While the uniform case provides a relatively straightforward solution using Gauss's law, non-uniform distributions require more sophisticated mathematical techniques. A thorough understanding of this topic is essential for anyone working in electromagnetism, physics, or engineering, impacting numerous applications ranging from everyday electronics to cutting-edge technologies. The principles explored here, especially the power of symmetry and Gauss's law, form the foundation for solving more complex electrostatic problems.
Latest Posts
Latest Posts
-
Ligaments Are Bundles Of Elastic And Collagen Fibers That
Apr 07, 2025
-
What Charge Does Sodium Ion Have
Apr 07, 2025
-
This Organelle Sorts And Packages Proteins
Apr 07, 2025
-
A Quadrilateral In Which The Diagonals Bisect Each Other
Apr 07, 2025
-
Units For Rate Constant K Third Order
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about Electric Field Of A Cylindrical Shell . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
