Domain And Range For Y 1 X
News Leon
Apr 01, 2025 · 5 min read
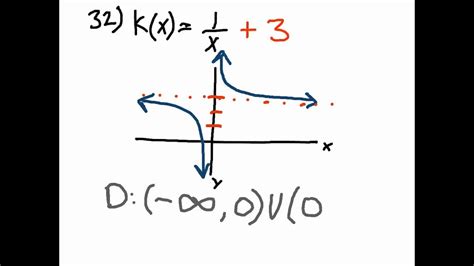
Table of Contents
Domain and Range: A Deep Dive into y = 1/x
Understanding the domain and range of a function is fundamental to mastering algebra and pre-calculus. This comprehensive guide will explore the domain and range of the reciprocal function, y = 1/x, in detail. We'll delve into the concepts, explore its graph, and consider how to apply this understanding to similar functions.
What are Domain and Range?
Before diving into the specifics of y = 1/x, let's solidify our understanding of domain and range.
-
Domain: The domain of a function is the set of all possible input values (often represented by 'x') for which the function is defined. In simpler terms, it's all the x-values you can plug into the function and get a valid output.
-
Range: The range of a function is the set of all possible output values (often represented by 'y') that the function can produce. It's all the y-values you'll see as a result of plugging in the x-values from the domain.
Analyzing the Function y = 1/x
The function y = 1/x, also known as the reciprocal function, presents a unique situation regarding its domain and range. Let's break it down:
Determining the Domain
The key to finding the domain of y = 1/x lies in identifying values of x that would make the function undefined. A fraction is undefined when its denominator is equal to zero. Therefore, we must find the value(s) of x that make the denominator, x, equal to zero.
The equation x = 0 is the only value that makes the denominator zero. This means that x cannot be 0. Therefore, the domain of y = 1/x is all real numbers except 0. We can express this using interval notation: (-∞, 0) U (0, ∞). This notation indicates all numbers from negative infinity to 0, excluding 0, and all numbers from 0 to positive infinity, excluding 0.
Determining the Range
To find the range, we consider all possible output values (y-values). Notice that as x approaches positive infinity, y approaches 0 from the positive side. Similarly, as x approaches negative infinity, y approaches 0 from the negative side. However, y can never actually equal 0 because there is no value of x that can make 1/x equal to 0.
Furthermore, for any non-zero value of y, we can find a corresponding x-value: x = 1/y. This means that every non-zero real number is included in the range. Therefore, the range of y = 1/x is all real numbers except 0. This can also be represented in interval notation as (-∞, 0) U (0, ∞).
Visualizing the Function: The Graph of y = 1/x
The graph of y = 1/x is a hyperbola. It consists of two separate branches, one in the first quadrant (where both x and y are positive) and one in the third quadrant (where both x and y are negative).
-
Asymptotes: The graph approaches, but never touches, the x-axis (y = 0) and the y-axis (x = 0). These lines are called asymptotes. The x-axis is a horizontal asymptote, and the y-axis is a vertical asymptote.
-
Symmetry: The graph is symmetrical with respect to the origin. This means that if you rotate the graph 180 degrees about the origin, it will look exactly the same.
The visual representation of the hyperbola clearly illustrates the domain and range. The graph never intersects the x or y axes, confirming that 0 is excluded from both the domain and the range.
Variations and Transformations: Exploring Related Functions
Understanding the domain and range of y = 1/x provides a foundation for analyzing related functions. Let's explore some variations:
y = a/x
Introducing a constant 'a' in the numerator changes the scaling of the graph vertically. The asymptotes remain at x = 0 and y = 0. The domain remains all real numbers except 0, and the range remains all real numbers except 0.
y = 1/(x + b)
Adding a constant 'b' to the denominator shifts the graph horizontally. The vertical asymptote shifts to x = -b. The horizontal asymptote remains y = 0. The domain is all real numbers except -b. The range remains all real numbers except 0.
y = 1/x + c
Adding a constant 'c' to the function shifts the graph vertically. The horizontal asymptote shifts to y = c. The vertical asymptote remains x = 0. The domain is all real numbers except 0. The range is all real numbers except c.
Combining Transformations: y = a/(x + b) + c
Combining these transformations produces a hyperbola with a vertical asymptote at x = -b, a horizontal asymptote at y = c, and a vertical scaling factor of 'a'. The domain will be all real numbers except -b, and the range will be all real numbers except c.
Real-World Applications of the Reciprocal Function
While y = 1/x might seem abstract, it has several practical applications:
-
Inverse Relationships: The function models inverse relationships between variables. For example, the time it takes to travel a certain distance is inversely proportional to speed.
-
Physics: The reciprocal function appears in many physics equations, such as the relationship between resistance and current in Ohm's Law (I = V/R).
-
Economics: In economics, inverse relationships are frequently observed. For example, the price of a commodity and the quantity demanded can exhibit an inverse relationship.
Advanced Considerations: Limits and Asymptotes
A deeper understanding of the domain and range of y = 1/x requires exploring the concept of limits. As x approaches 0 from the positive side, y approaches positive infinity (lim_(x→0⁺) 1/x = ∞). As x approaches 0 from the negative side, y approaches negative infinity (lim_(x→0⁻) 1/x = -∞). This behavior defines the vertical asymptote at x = 0. Similarly, as x approaches positive or negative infinity, y approaches 0, defining the horizontal asymptote at y = 0.
Conclusion: Mastering the Domain and Range of y = 1/x
Understanding the domain and range of y = 1/x is crucial for a solid grasp of function analysis. By analyzing the function's definition, visualizing its graph, and exploring its transformations, you gain a deeper appreciation of its behavior and its relevance to various fields. Remember that identifying values that make the denominator zero is key to determining the domain, while examining the function's behavior as x approaches infinity and the potential output values helps define the range. This understanding will serve as a strong foundation for tackling more complex functions in your mathematical journey.
Latest Posts
Latest Posts
-
Which Of The Following Combinations Is Correct
Apr 02, 2025
-
How Do You Find The Boiling Point Of A Solution
Apr 02, 2025
-
Balance Equation Fes2 O2 Fe2o3 So2
Apr 02, 2025
-
Which Is Not A Physical Property
Apr 02, 2025
-
Australia Is The Worlds Leading Producer Of
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Domain And Range For Y 1 X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
