Domain And Range For X 3
News Leon
Mar 31, 2025 · 6 min read
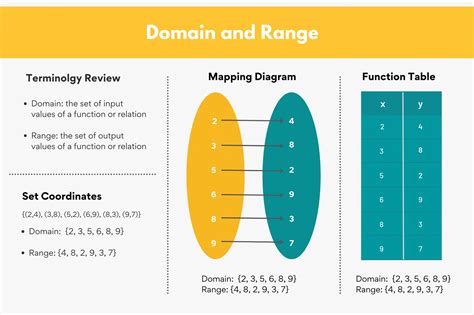
Table of Contents
Understanding Domain and Range: A Deep Dive into f(x) = x³
The concept of domain and range is fundamental to understanding functions in mathematics. While seemingly simple at first glance, a thorough grasp of these concepts is crucial for tackling more advanced topics in calculus, algebra, and beyond. This comprehensive guide will explore the domain and range of the cubic function, f(x) = x³, in detail, providing examples and explanations to solidify your understanding. We'll delve into various representations – graphical, algebraic, and tabular – to ensure a multifaceted comprehension.
What are Domain and Range?
Before we dive into the specifics of f(x) = x³, let's establish a clear definition of domain and range.
Domain: The domain of a function refers to the set of all possible input values (x-values) for which the function is defined. In simpler terms, it's the set of all x-values that you can "plug into" the function and get a valid output.
Range: The range of a function is the set of all possible output values (y-values) that the function can produce. It's the collection of all values the function can "reach" given its defined domain.
Exploring the Domain of f(x) = x³
The beauty of the cubic function, f(x) = x³, lies in its simplicity and its unrestricted domain. Unlike some functions that have limitations on their input values (e.g., functions with square roots or denominators), the cubic function is defined for all real numbers.
Why is the domain of f(x) = x³ all real numbers?
There are no restrictions on the values of 'x' that can be cubed. You can cube positive numbers, negative numbers, zero, and even irrational numbers like π. The result will always be a real number. Therefore, the domain of f(x) = x³ is:
(-∞, ∞) or (-∞, +∞) or all real numbers
This notation signifies that the domain extends infinitely in both the positive and negative directions along the x-axis.
Visualizing the Domain: The Graph of f(x) = x³
The graph of f(x) = x³ is a smooth, continuous curve that extends infinitely in both directions along the x-axis. This visual representation reinforces the idea that there are no gaps or breaks in the domain; you can find a corresponding y-value for any x-value you choose.
Understanding the Range of f(x) = x³
Just like its domain, the range of f(x) = x³ is also unrestricted. This means that for every real number 'y', there exists a real number 'x' such that f(x) = y.
Why is the range of f(x) = x³ all real numbers?
Consider the inverse of the cubic function: ∛y. The cube root of any real number is also a real number. This implies that for every y-value, there's a corresponding x-value that satisfies the equation f(x) = y. This one-to-one correspondence between the input and output demonstrates that the range is also unbounded.
Therefore, the range of f(x) = x³ is:
(-∞, ∞) or (-∞, +∞) or all real numbers
This indicates that the function's output values stretch infinitely in both the positive and negative directions along the y-axis.
Visualizing the Range: The Graph of f(x) = x³
The graph of f(x) = x³ visually confirms this unrestricted range. The curve extends infinitely in both the upward and downward directions along the y-axis, demonstrating that the function can produce any real number as an output.
Analyzing Domain and Range Through Different Representations
To further solidify your understanding, let's examine the domain and range of f(x) = x³ using different representations:
1. Algebraic Representation:
The algebraic representation, f(x) = x³, directly shows the absence of any restrictions on the input (x). There are no square roots, denominators, or logarithmic functions that would limit the acceptable x-values. Similarly, solving for x (x = ∛y) demonstrates that any y-value will yield a real x-value, indicating an unrestricted range.
2. Tabular Representation:
A table can illustrate the domain and range by showing sample input and output values. However, a table can only show a limited selection of values and cannot fully represent the infinite domain and range.
| x | f(x) = x³ |
|---|---|
| -2 | -8 |
| -1 | -1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
| 10 | 1000 |
| -10 | -1000 |
Even this limited table suggests that the function will produce outputs for any input chosen.
3. Graphical Representation:
The graph of f(x) = x³ provides the most intuitive visualization of the domain and range. The curve's continuous and unbounded nature along both axes clearly depicts the infinite extent of both the domain and range.
Comparing f(x) = x³ with Functions with Restricted Domains and Ranges
Understanding the unrestricted domain and range of f(x) = x³ becomes even clearer when contrasted with functions that do have restrictions:
1. Square Root Functions: Consider f(x) = √x. The domain is restricted to non-negative numbers (x ≥ 0) because you cannot take the square root of a negative number and obtain a real result. The range, however, is all non-negative real numbers (y ≥ 0).
2. Rational Functions: Consider f(x) = 1/x. The domain excludes x = 0, as division by zero is undefined. The range also excludes y = 0, as there is no x-value that will make the function equal to zero.
3. Logarithmic Functions: Consider f(x) = log(x). The domain is restricted to positive numbers (x > 0) because the logarithm of a non-positive number is undefined. The range, however, is all real numbers.
These examples highlight that the unrestricted domain and range of f(x) = x³ are a special and important characteristic, not shared by all functions.
Applications of Understanding Domain and Range
Understanding domain and range is not merely an academic exercise; it has practical implications in various fields:
- Data Analysis: When analyzing data, identifying the domain and range helps determine the scope and limitations of the data set.
- Modeling Real-World Phenomena: Many real-world phenomena can be modeled using mathematical functions. Understanding the domain and range of these functions helps interpret the model's predictions and limitations. For example, in physics, the domain might represent physically possible values, like time or distance, while the range would be the associated physical quantities.
- Computer Programming: In programming, understanding domain and range is critical for ensuring that functions are used correctly and avoid errors like division by zero or taking the square root of a negative number. It is crucial for data validation and error handling.
- Economics and Finance: Functions modeling economic or financial systems often have restricted domains representing realistic constraints, such as non-negative quantities or budgets.
Conclusion
The cubic function, f(x) = x³, provides a clean and instructive example of a function with an unrestricted domain and range. Mastering the concepts of domain and range for this fundamental function lays a strong foundation for understanding more complex functions and their applications in diverse fields. Remember that visualizing the function through graphs, analyzing it algebraically, and considering its tabular representation will help you develop a comprehensive understanding of this crucial aspect of function analysis. By thoroughly grasping these core concepts, you’ll be well-equipped to tackle more advanced mathematical concepts and applications with confidence.
Latest Posts
Latest Posts
-
Experiment To Show That Chlorophyll Is Necessary For Photosynthesis Meritnation
Apr 02, 2025
-
What Is The Difference Between Heterochromatin And Euchromatin
Apr 02, 2025
-
In Order List The Steps Of The Scientific Method
Apr 02, 2025
-
How To Find Instantaneous Rate Of Change From A Table
Apr 02, 2025
-
Which Of The Following Will Have The Highest Boiling Point
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Domain And Range For X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
