Blocks A And B Of Masses Ma And Mb
News Leon
Mar 31, 2025 · 7 min read
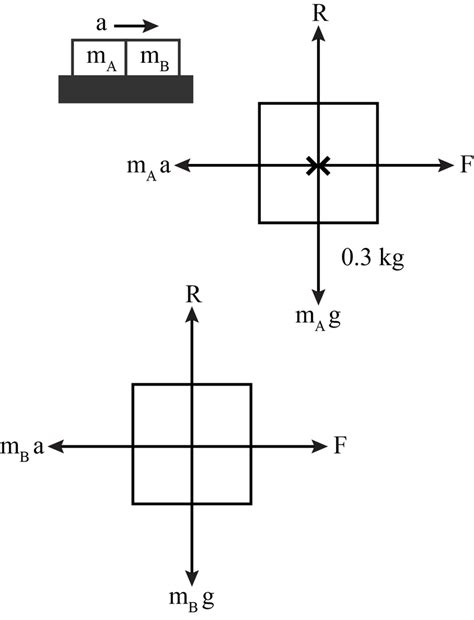
Table of Contents
Blocks A and B: A Deep Dive into Newtonian Mechanics
Understanding the interactions between two blocks, A and B, with masses m<sub>a</sub> and m<sub>b</sub>, respectively, is fundamental to grasping core concepts in Newtonian mechanics. This seemingly simple system provides a rich landscape for exploring forces, friction, acceleration, and energy transfer. This article will delve into various scenarios involving blocks A and B, analyzing their motion under different conditions, focusing on both theoretical understanding and practical applications.
Analyzing Static and Kinetic Friction
Before examining specific scenarios, it's crucial to understand the role of friction. Friction is a force that opposes motion between surfaces in contact. We distinguish between two main types:
Static Friction
Static friction (F<sub>s</sub>) acts when the blocks are at rest relative to each other. It prevents any motion from starting. The maximum static friction force is given by:
F<sub>s,max</sub> = μ<sub>s</sub>N
where:
- μ<sub>s</sub> is the coefficient of static friction (a dimensionless constant depending on the surfaces in contact)
- N is the normal force between the blocks (the force perpendicular to the contact surface).
Kinetic Friction
Once the blocks start moving relative to each other, kinetic friction (F<sub>k</sub>) comes into play. It opposes the motion and is given by:
F<sub>k</sub> = μ<sub>k</sub>N
where:
- μ<sub>k</sub> is the coefficient of kinetic friction (usually less than μ<sub>s</sub>)
- N is again the normal force.
It's important to note that both μ<sub>s</sub> and μ<sub>k</sub> are experimentally determined values and depend heavily on the materials involved. A smooth surface will have lower coefficients of friction compared to a rough surface.
Scenario 1: Blocks on a Horizontal Surface
Let's consider blocks A and B resting on a horizontal frictionless surface. A force, F, is applied to block A, which is in contact with block B.
Analyzing the Forces
- Force F: The applied force acting on block A.
- Force of Contact (F<sub>c</sub>): The force block A exerts on block B (and vice-versa, due to Newton's Third Law).
- Acceleration (a): Both blocks will have the same acceleration (assuming they remain in contact).
Applying Newton's Second Law (F=ma) to each block:
- For block A: F - F<sub>c</sub> = m<sub>a</sub>a
- For block B: F<sub>c</sub> = m<sub>b</sub>a
We can solve these two equations simultaneously to find the acceleration (a) and the force of contact (F<sub>c</sub>):
- a = F / (m<sub>a</sub> + m<sub>b</sub>)
- F<sub>c</sub> = m<sub>b</sub>F / (m<sub>a</sub> + m<sub>b</sub>)
This demonstrates that the acceleration of the system is inversely proportional to the total mass and directly proportional to the applied force. The force of contact is proportional to the mass of block B and the applied force.
Introducing Friction
If we introduce friction between the blocks and the surface, or between the blocks themselves, the equations become more complex. We need to account for the frictional forces acting on each block, which will depend on the normal force (equal to the weight of the block in this case) and the coefficient of friction. The acceleration will be reduced due to the opposing forces of friction.
Scenario 2: Blocks on an Inclined Plane
Placing the blocks on an inclined plane adds another dimension to the problem. Now, gravity plays a significant role, contributing to the forces acting on the blocks.
Forces on an Inclined Plane
- Gravitational Force (mg): Acts vertically downwards. This needs to be resolved into components parallel and perpendicular to the plane.
- Normal Force (N): Acts perpendicular to the inclined plane.
- Frictional Force (F<sub>f</sub>): Acts parallel to the plane, opposing motion.
The analysis becomes significantly more intricate, requiring resolving forces into components and careful consideration of the direction of motion. The angle of inclination plays a crucial role in determining the acceleration and the forces involved. Different scenarios can arise depending on the angle and the coefficients of friction.
Analyzing different friction scenarios
-
Frictionless Inclined Plane: If the inclined plane is frictionless, the acceleration down the plane is determined solely by the component of gravity parallel to the plane.
-
With Friction: If friction is present, the net force down the plane is the difference between the component of gravity parallel to the plane and the frictional force. The acceleration is reduced. There's a critical angle beyond which the blocks will not slide even without an applied force, owing to the balance between the component of gravity and the maximum static friction.
Scenario 3: Pulley System with Blocks A and B
Consider a system where block A and block B are connected by a massless, inextensible string that passes over a frictionless pulley.
Forces and Acceleration
- Tension (T): The tension in the string is the same throughout (assuming a massless, inextensible string).
- Gravitational Force (m<sub>a</sub>g, m<sub>b</sub>g): Acts on each block.
- Acceleration (a): The blocks will have the same magnitude of acceleration, but in opposite directions.
Assuming block A is heavier, it will accelerate downwards while block B accelerates upwards. Applying Newton's Second Law to each block:
- For block A: m<sub>a</sub>g - T = m<sub>a</sub>a
- For block B: T - m<sub>b</sub>g = m<sub>b</sub>a
Solving these equations for the acceleration (a) and the tension (T):
- a = (m<sub>a</sub> - m<sub>b</sub>)g / (m<sub>a</sub> + m<sub>b</sub>)
- T = 2m<sub>a</sub>m<sub>b</sub>g / (m<sub>a</sub> + m<sub>b</sub>)
This shows that the acceleration depends on the difference in masses, while the tension depends on both masses. If m<sub>a</sub> = m<sub>b</sub>, the acceleration is zero, and the system is in equilibrium.
Introducing Friction in Pulley System
Adding friction to the pulley or to the surfaces the blocks are in contact with further complicates the system. The acceleration will be reduced, and the tension in the string will change. The calculations will involve accounting for the frictional torques on the pulley and the frictional forces on the blocks.
Scenario 4: Blocks Connected by a Spring
If blocks A and B are connected by a spring, the system introduces the concept of elastic potential energy.
Hooke's Law and Energy Conservation
The force exerted by the spring is governed by Hooke's Law:
F<sub>s</sub> = -kx
where:
- k is the spring constant (a measure of the spring's stiffness)
- x is the extension or compression of the spring from its equilibrium position.
The negative sign indicates that the spring force opposes the displacement. Analyzing the motion requires applying conservation of energy principles, considering the interplay between kinetic energy, potential energy (both gravitational and elastic), and work done by external forces.
Advanced Considerations
The scenarios discussed above represent fundamental cases. More complex situations can involve:
- Multiple forces acting on the blocks.
- Varying coefficients of friction.
- Non-uniform acceleration.
- Systems with more than two blocks.
- The introduction of inclined planes and pulley systems simultaneously.
These scenarios require a deeper understanding of vector calculus and often necessitate numerical methods for solving the equations of motion.
Conclusion
Analyzing the motion of blocks A and B under different conditions provides a powerful framework for understanding fundamental principles in Newtonian mechanics. Starting with basic scenarios and gradually introducing complexity allows for a progressive mastery of concepts such as forces, friction, acceleration, energy conservation, and the application of Newton's Laws. By systematically dissecting these systems, we can build a strong foundation for tackling more advanced problems in classical mechanics. Remember to always carefully define your system, identify all forces acting on each body, and apply Newton's Laws appropriately. The ability to solve these problems provides a cornerstone for understanding more complex systems in physics and engineering.
Latest Posts
Latest Posts
-
Compare And Contrast Evaporation And Boiling
Apr 01, 2025
-
1 Mole Of Carbon In Grams
Apr 01, 2025
-
What Is The Charge On A Sulfide Ion
Apr 01, 2025
-
What Is Not A Function Of The Lymphatic System
Apr 01, 2025
-
Who Has Hemophilia In The Pedigree That Is Shown
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Blocks A And B Of Masses Ma And Mb . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
