An Earth Satellite Moves In A Circular Orbit
News Leon
Mar 17, 2025 · 6 min read
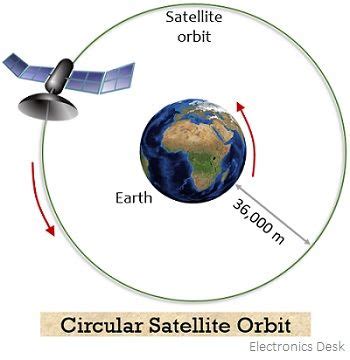
Table of Contents
An Earth Satellite Moves in a Circular Orbit: A Deep Dive into Orbital Mechanics
Understanding how an Earth satellite moves in a circular orbit is fundamental to comprehending space exploration, communication technologies, and even our understanding of gravity. This seemingly simple concept underpins complex satellite missions, from GPS navigation to weather forecasting and scientific observation. This article provides a comprehensive exploration of the physics behind circular orbits, examining the forces at play, the key orbital parameters, and the practical applications of this knowledge.
The Physics of Circular Orbits: A Balancing Act
At its core, a satellite in a circular orbit around the Earth is a beautiful demonstration of balanced forces. The satellite continuously falls towards the Earth due to gravity, yet it never actually gets any closer. This seemingly paradoxical situation is resolved by understanding the interplay between gravity and the satellite's tangential velocity.
Gravity: The Unsung Hero
Gravity, the force of attraction between two objects with mass, is the primary force governing a satellite's orbit. Newton's Law of Universal Gravitation states that the force of gravity (F<sub>g</sub>) between two objects is directly proportional to the product of their masses (m<sub>1</sub> and m<sub>2</sub>) and inversely proportional to the square of the distance (r) between their centers:
F<sub>g</sub> = G * (m<sub>1</sub> * m<sub>2</sub>) / r<sup>2</sup>
Where G is the gravitational constant. In the context of an Earth satellite, m<sub>1</sub> represents the Earth's mass, m<sub>2</sub> represents the satellite's mass, and r is the distance between the Earth's center and the satellite.
Centripetal Force: The Orbital Stabilizer
For a satellite to maintain a circular orbit, it must possess a specific velocity. This velocity creates a centripetal force (F<sub>c</sub>), which constantly pulls the satellite towards the center of the Earth. This force is given by:
F<sub>c</sub> = m<sub>2</sub> * v<sup>2</sup> / r
Where m<sub>2</sub> is the satellite's mass, v is its orbital velocity, and r is the orbital radius.
The Equilibrium Condition: A Perfect Balance
For a stable circular orbit, the centripetal force must exactly balance the gravitational force. This equilibrium condition is expressed as:
F<sub>g</sub> = F<sub>c</sub>
This equation allows us to derive crucial relationships between a satellite's orbital velocity, its orbital radius, and the Earth's mass.
Key Orbital Parameters: Defining the Satellite's Path
Several key parameters precisely define a satellite's circular orbit:
Orbital Radius (r): The Distance to the Center
The orbital radius is the distance between the center of the Earth and the satellite. It dictates the altitude of the satellite above the Earth's surface. A larger orbital radius implies a higher altitude and a slower orbital velocity.
Orbital Velocity (v): The Speed of the Satellite
The orbital velocity is the speed at which the satellite travels along its circular path. It's directly related to the orbital radius and the Earth's gravitational pull. A smaller orbital radius results in a higher orbital velocity to counteract the stronger gravitational force.
Orbital Period (T): The Time for One Revolution
The orbital period is the time it takes for the satellite to complete one full revolution around the Earth. It's related to the orbital velocity and the orbital radius. Kepler's Third Law provides a mathematical relationship between the orbital period and the orbital radius.
Altitude (h): The Height Above the Earth's Surface
The altitude is the distance of the satellite above the Earth's surface. It's easily calculated by subtracting the Earth's radius from the orbital radius:
h = r - R<sub>E</sub>
Where R<sub>E</sub> is the Earth's radius.
Applications of Circular Orbits: Real-World Implications
The concept of circular orbits has far-reaching applications in various fields:
Global Positioning System (GPS): Precise Navigation
GPS satellites utilize precisely controlled circular orbits to provide accurate location data worldwide. The precise timing of their signals, dictated by their consistent orbital parameters, is crucial for determining position.
Geostationary Satellites: Constant Coverage
Geostationary satellites orbit the Earth at an altitude of approximately 35,786 kilometers, matching the Earth's rotational period. This allows them to remain stationary above a specific point on the Earth's surface, providing continuous coverage for communication and broadcasting. This is a special case of a circular orbit where the orbital period precisely matches the Earth's rotational period.
Earth Observation Satellites: Monitoring Our Planet
Numerous Earth observation satellites use circular orbits at varying altitudes to monitor weather patterns, land use changes, and environmental conditions. The choice of orbit depends on the specific application, with lower orbits providing higher resolution images but requiring more frequent passes over the area of interest.
Scientific Research Satellites: Exploring Space
Scientific research satellites utilize circular orbits to conduct experiments and observations in space. These orbits can be tailored to specific needs, such as minimizing atmospheric drag or optimizing access to specific regions of space.
Beyond Circular Orbits: Exploring More Complex Trajectories
While circular orbits provide a simple and elegant model for understanding satellite motion, many satellites utilize more complex elliptical or even highly irregular orbits to optimize their mission objectives. Understanding circular orbits forms the foundational knowledge for comprehending these more complex orbital maneuvers.
Factors Affecting Orbital Stability: Perturbations and Corrections
While the idealized model of a circular orbit assumes a perfectly uniform gravitational field, real-world orbits are subject to various perturbations. These perturbations include:
- Non-spherical Earth: The Earth isn't a perfect sphere; its slightly oblate shape introduces gravitational variations that affect satellite orbits.
- Atmospheric drag: At lower altitudes, atmospheric drag exerts a frictional force on satellites, slowing them down and causing orbital decay.
- Solar radiation pressure: The pressure exerted by sunlight can subtly alter a satellite's orbit over time.
- Gravitational influence of the sun and moon: The gravitational pull of the sun and moon also causes minor perturbations in satellite orbits.
To maintain the desired orbit, satellites often require occasional adjustments through orbital maneuvers, using onboard thrusters to counteract these perturbations and maintain the intended circular path.
Conclusion: The Enduring Importance of Circular Orbits
The study of satellites moving in circular orbits remains a cornerstone of space science and technology. This seemingly simple concept provides the basis for understanding the complexities of orbital mechanics, enabling the development of sophisticated satellite systems that play a crucial role in modern society. From GPS navigation and communication systems to Earth observation and scientific research, circular orbits underpin numerous critical applications, highlighting the enduring significance of this fundamental aspect of orbital mechanics. The continuing advancements in our understanding of orbital dynamics promise even more innovative applications in the future, pushing the boundaries of space exploration and our knowledge of the universe.
Latest Posts
Latest Posts
-
Mountain Range Separating Europe From Asia
Mar 17, 2025
-
200 Cm Equals How Many M
Mar 17, 2025
-
How Many Yards In 90 Inches
Mar 17, 2025
-
Explain Why Plants Are Called Producers
Mar 17, 2025
-
What Is The Systematic Name Of Mg No3 2
Mar 17, 2025
Related Post
Thank you for visiting our website which covers about An Earth Satellite Moves In A Circular Orbit . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
