All Squares Are Rhombuses True Or False
News Leon
Apr 05, 2025 · 5 min read
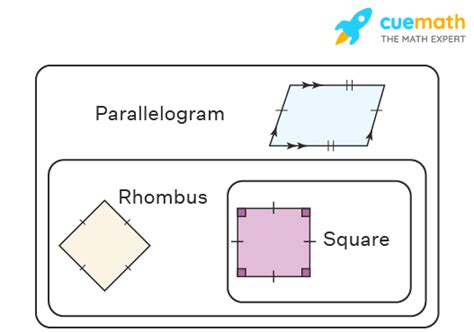
Table of Contents
All Squares Are Rhombuses: True or False? A Deep Dive into Quadrilateral Geometry
The statement "All squares are rhombuses" is true. Understanding why requires a journey into the fascinating world of quadrilateral geometry, specifically exploring the defining characteristics of squares and rhombuses. This article will delve into the properties of each shape, comparing and contrasting them to definitively prove the veracity of the statement and enhance your understanding of geometric relationships. We'll also touch upon related concepts and explore practical applications of this knowledge.
Understanding Quadrilaterals: A Foundation
Before diving into squares and rhombuses, let's establish a foundational understanding of quadrilaterals. A quadrilateral is simply a polygon with four sides. Many different types of quadrilaterals exist, each defined by specific properties and relationships between their sides and angles. Some common examples include:
- Trapezoids: Quadrilaterals with at least one pair of parallel sides.
- Parallelograms: Quadrilaterals with two pairs of parallel sides.
- Rectangles: Parallelograms with four right angles.
- Rhombuses: Parallelograms with four congruent sides.
- Squares: Parallelograms with four congruent sides and four right angles.
Defining a Rhombus: Key Characteristics
A rhombus is a special type of parallelogram. Its defining characteristics are:
- Four congruent sides: All four sides of a rhombus have equal length. This is the most crucial characteristic that distinguishes a rhombus from other parallelograms.
- Opposite sides are parallel: Like all parallelograms, opposite sides of a rhombus are parallel to each other.
- Opposite angles are equal: Opposite angles within a rhombus are congruent (have the same measure).
- Consecutive angles are supplementary: Consecutive angles (angles next to each other) add up to 180 degrees.
- Diagonals bisect each other: The diagonals of a rhombus intersect at a point that divides each diagonal into two equal segments.
- Diagonals are perpendicular bisectors: The diagonals of a rhombus intersect at right angles and bisect each other.
Defining a Square: The Ultimate Parallelogram
A square is a highly specialized quadrilateral. It inherits all the properties of a parallelogram, a rectangle, and a rhombus, making it the most symmetrical of all quadrilaterals. Its defining characteristics include:
- Four congruent sides: Like a rhombus, all four sides of a square are equal in length.
- Four right angles: All four angles of a square measure 90 degrees. This is the key difference between a square and a rhombus.
- Opposite sides are parallel: As with all parallelograms, opposite sides are parallel.
- Opposite angles are equal: Opposite angles are congruent.
- Diagonals bisect each other: The diagonals intersect at a point that divides each diagonal into two equal segments.
- Diagonals are perpendicular bisectors: The diagonals intersect at right angles and bisect each other.
- Diagonals are congruent: Unlike a rhombus, a square's diagonals are also equal in length.
Why All Squares Are Rhombuses: The Proof
The statement "All squares are rhombuses" is true because a square satisfies all the defining conditions of a rhombus. Let's review:
A rhombus requires four congruent sides and opposite sides to be parallel. A square, by definition, possesses four congruent sides (all sides are equal in length) and its opposite sides are indeed parallel. Therefore, a square inherently fulfills all the necessary criteria to be classified as a rhombus. It's a subset of the rhombus family. However, not all rhombuses are squares. A rhombus only needs four equal sides; its angles don't have to be right angles.
In essence, a square is a rhombus with the added constraint of having four right angles. This makes a square a more specific, specialized case within the broader category of rhombuses.
Venn Diagram Representation
A Venn diagram visually clarifies the relationship between squares and rhombuses:
Imagine two overlapping circles. One circle represents all rhombuses, and the other represents all squares. The circle representing squares is entirely contained within the circle representing rhombuses. This visually demonstrates that all squares are rhombuses, but not all rhombuses are squares. The overlapping region represents the set of all squares, which is a subset of the set of all rhombuses.
Real-World Applications: Where Do We See Squares and Rhombuses?
Understanding the relationship between squares and rhombuses is more than just an academic exercise. These shapes appear frequently in various aspects of our lives:
- Architecture and Construction: Squares are fundamental in building design, from windows and doors to the overall structure of buildings. Rhombuses, while less common, can be found in some architectural features and supporting structures.
- Art and Design: Artists utilize squares and rhombuses in creating visual balance and patterns. Tessellations often incorporate these shapes.
- Engineering: Squares and rhombuses appear in engineering designs, particularly in mechanical systems and structural frameworks.
- Games and Puzzles: Many games and puzzles feature these shapes, stimulating spatial reasoning and problem-solving skills.
Beyond Squares and Rhombuses: Exploring Other Quadrilaterals
Expanding our understanding of squares and rhombuses allows us to appreciate the broader relationships within the quadrilateral family. We can further classify and categorize various quadrilaterals based on their shared properties. For example:
- Rectangles: All rectangles are parallelograms but not all parallelograms are rectangles (rectangles require 4 right angles). Squares are special cases of rectangles.
- Trapezoids: A trapezoid only requires one pair of parallel sides. Neither squares nor rhombuses are trapezoids unless they are degenerate cases (sides overlapping).
- Kites: A kite has two pairs of adjacent sides that are congruent.
Understanding these relationships helps to build a strong foundation in geometric reasoning and problem-solving.
Conclusion: A Firm Grasp on Geometric Relationships
The statement "All squares are rhombuses" is unequivocally true. This understanding is not just about memorizing a fact; it’s about grasping the fundamental properties that define different geometric shapes and recognizing the hierarchical relationships between them. By exploring the unique characteristics of squares and rhombuses and comparing them within the broader context of quadrilaterals, we gain a deeper appreciation for the elegance and logic of geometry. This knowledge extends beyond the classroom, finding applications in numerous fields and contributing to our ability to analyze and understand the world around us. The ability to discern these geometric relationships enhances critical thinking and problem-solving skills, valuable assets in various aspects of life.
Latest Posts
Latest Posts
-
You Should Always Assign The Needs Met Rating Before
Apr 06, 2025
-
Which Is The Most Densely Populated Continent
Apr 06, 2025
-
Average Velocity On Velocity Time Graph
Apr 06, 2025
-
The First Scientist To Observe Cells With A Microscope Was
Apr 06, 2025
-
What Happens When The Price Of A Complementary Good Increases
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about All Squares Are Rhombuses True Or False . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
