All Isosceles Right Triangles Are Similar
News Leon
Apr 04, 2025 · 5 min read
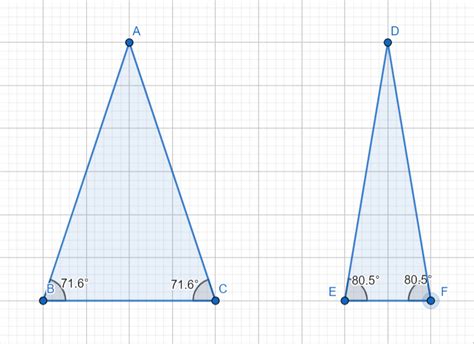
Table of Contents
All Isosceles Right Triangles Are Similar: A Comprehensive Exploration
Isosceles right triangles, also known as 45-45-90 triangles, hold a unique position in geometry. Their inherent properties lead to a fascinating conclusion: all isosceles right triangles are similar. This article will delve deep into this statement, exploring the underlying concepts of similarity, the characteristics of isosceles right triangles, and proving definitively why this geometric truth holds. We'll also explore some practical applications and further considerations.
Understanding Similarity in Triangles
Before diving into the specifics of isosceles right triangles, let's establish a firm understanding of what constitutes similar triangles. Two triangles are considered similar if they meet one of the following criteria:
-
AA (Angle-Angle): If two angles of one triangle are congruent to two angles of another triangle, then the triangles are similar. This is because the third angles must also be congruent (since the sum of angles in a triangle is always 180°).
-
SSS (Side-Side-Side): If the ratio of corresponding sides of two triangles are equal, then the triangles are similar. This means that the sides of one triangle are proportional to the sides of the other.
-
SAS (Side-Angle-Side): If two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent, then the triangles are similar.
Defining Isosceles Right Triangles
An isosceles right triangle is a triangle that possesses two key characteristics:
- Isosceles: It has two sides of equal length (these are called the legs).
- Right Triangle: It contains one right angle (90°).
The combination of these properties dictates that the other two angles must each measure 45° (since the angles in a triangle sum to 180°). This consistent angular arrangement is the cornerstone of their similarity.
Proof: All Isosceles Right Triangles are Similar
We can demonstrate that all isosceles right triangles are similar using the AA similarity postulate. Let's consider two isosceles right triangles, Triangle A and Triangle B.
- Triangle A: Has legs of length 'a' and hypotenuse of length 'a√2'.
- Triangle B: Has legs of length 'b' and hypotenuse of length 'b√2'.
Both triangles possess the following angles:
- One 90° angle
- Two 45° angles
Because both Triangle A and Triangle B share two congruent angles (a 90° angle and two 45° angles), they satisfy the AA similarity postulate. Therefore, Triangle A is similar to Triangle B. This logic applies to any two isosceles right triangles; the specific lengths of their sides are irrelevant—the consistent 45-45-90 angle arrangement guarantees their similarity.
Visualizing the Similarity
Imagine scaling an isosceles right triangle. Whether you enlarge it or shrink it, the resulting triangle will still maintain the same 45-45-90 angle ratios. The ratio of the sides will remain constant, further emphasizing their similarity. You are essentially creating a larger or smaller version of the original, maintaining the same shape but with different dimensions. This scalability is a defining characteristic of similar shapes.
Further Mathematical Exploration
The ratio of the sides in an isosceles right triangle is always constant. The ratio of the leg to the hypotenuse is always 1:√2, or approximately 1:1.414. This constant ratio further reinforces the concept of similarity. No matter the size of the isosceles right triangle, this ratio will remain unchanged, showcasing the proportional relationship between the sides.
We can also explore this using trigonometry. In an isosceles right triangle:
- sin(45°) = cos(45°) = 1/√2
- tan(45°) = 1
These constant trigonometric ratios are independent of the size of the triangle, proving the consistency of proportions across all isosceles right triangles.
Practical Applications
The consistent properties of isosceles right triangles find applications in various fields:
-
Construction: Understanding isosceles right triangles is crucial in building projects requiring precise angles and measurements. Roof structures, stair designs, and foundation layouts often utilize the principles of 45-45-90 triangles for stability and accuracy.
-
Engineering: In engineering designs involving structural components, isosceles right triangles play a significant role. Calculations involving forces, stresses, and stability often rely on the predictable properties of these triangles.
-
Computer Graphics and Game Development: The simplicity and predictability of isosceles right triangles make them useful in computer graphics. Generating and manipulating 2D and 3D shapes often uses these triangles as fundamental building blocks, ensuring consistent scaling and rotation.
-
Navigation and Surveying: Isosceles right triangles can assist in determining distances and angles in surveying and navigation. Their predictable angles and side ratios make calculations simpler and more efficient.
Beyond Isosceles Right Triangles: A Broader Perspective
While this article focuses on isosceles right triangles, the concept of similarity extends to all triangles and geometric shapes. Understanding similarity is fundamental to geometry and has numerous applications in various fields. The principles discussed here can be extended to understand the similarity of other types of triangles, such as equilateral triangles or scalene triangles, although the conditions for similarity will differ.
Conclusion: The Significance of Similarity
The fact that all isosceles right triangles are similar is not just a geometric curiosity; it's a testament to the elegance and consistency of mathematical principles. This property simplifies calculations, provides predictability in designs, and underlies many practical applications across various disciplines. Understanding this fundamental geometric concept is crucial for anyone working with angles, shapes, and proportions. The consistent 45-45-90 degree angles and the constant ratio of sides guarantee the similarity of all isosceles right triangles, making them a unique and useful shape in mathematics and the real world. This consistent nature allows for simplification in various calculations and applications, highlighting the importance of understanding similar figures in geometry. The inherent properties of isosceles right triangles make them a fundamental building block in various fields, solidifying their importance in mathematics and its practical applications.
Latest Posts
Latest Posts
-
What Major Element Is Found In Chlorophyll
Apr 05, 2025
-
Antibodies Are Secreted From Which Type Of Cell
Apr 05, 2025
-
Impulse Conduction Is Fastest In Neurons That Are
Apr 05, 2025
-
Largest Organelle Of The Cell Contains Dna
Apr 05, 2025
-
How Many Molecules Are In 1 Mole Of Water
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about All Isosceles Right Triangles Are Similar . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
