A Uniform Spherical Shell Of Mass M
News Leon
Mar 29, 2025 · 5 min read
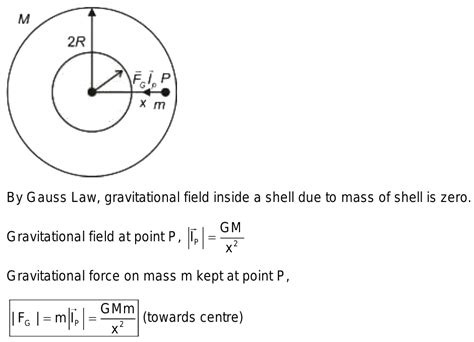
Table of Contents
A Uniform Spherical Shell of Mass m: Exploring its Gravitational and Mechanical Properties
A uniform spherical shell, possessing a mass 'm' and a consistent density throughout its structure, presents a fascinating case study in physics, encompassing principles of both gravitation and mechanics. Its unique properties, particularly concerning gravitational fields and potential, offer valuable insights into celestial mechanics and theoretical physics. This comprehensive exploration will delve into the intricacies of this seemingly simple object, uncovering its surprising characteristics and applications.
Gravitational Field of a Uniform Spherical Shell
One of the most striking features of a uniform spherical shell is its gravitational field. Unlike a solid sphere, where the gravitational field increases linearly with distance from the center (for points inside the sphere), the field generated by a spherical shell exhibits a distinct duality:
Outside the Shell:
For points located outside the shell, the gravitational field behaves as if the entire mass 'm' were concentrated at the center of the shell. This crucial finding simplifies many calculations in astrophysics. The gravitational field strength (g) at a distance 'r' from the center (where r > R, R being the radius of the shell) is given by:
g = GM/r²
where G is the universal gravitational constant and M is the mass of the shell (m). This equation is identical to the gravitational field of a point mass, highlighting the shell's remarkable ability to effectively concentrate its gravitational influence at its center when observed from the outside. This is a consequence of the symmetry of the mass distribution. The contributions from different parts of the shell cancel out in all directions except radially.
Inside the Shell:
This is where the spherical shell reveals its most counterintuitive property: the gravitational field inside the shell is zero. No matter where you are located within the hollow space enclosed by the shell, the gravitational force acting upon you is precisely zero. This remarkable result stems from the symmetrical distribution of mass. The gravitational pull from different sections of the shell perfectly cancels each other out, resulting in a net force of zero.
This concept is crucial in understanding the behavior of objects within larger celestial bodies. Consider a planet. While the overall gravitational force on an object inside the planet is non-zero due to the density variation, understanding the shell theorem provides a framework for analyzing gravitational contributions from different layers. Each concentric spherical shell, theoretically, contributes zero gravitational force on the points lying within. The overall gravitational pull at the interior point results from the mass of the shells lying within it.
This "zero-gravity" interior is a powerful theoretical tool in numerous areas. It simplifies the study of gravitational effects within larger spherical bodies, and serves as a foundational concept in understanding the behavior of matter under varying gravitational conditions.
Gravitational Potential of a Uniform Spherical Shell
Complementary to the gravitational field is the concept of gravitational potential. The gravitational potential (V) represents the potential energy per unit mass associated with the gravitational field. For a uniform spherical shell, the potential exhibits a similar duality as the field:
Outside the Shell:
The gravitational potential outside the shell is given by:
V = -GM/r
This again mirrors the potential of a point mass located at the center of the shell, reinforcing the point-mass equivalence from an external perspective.
Inside the Shell:
Inside the shell, the potential is constant and equal to:
V = -GM/R
The potential remains constant at any point inside the shell. This constant potential implies that no work is needed to move an object within the shell's interior, a direct consequence of the zero gravitational field within.
Mechanical Properties of a Uniform Spherical Shell
Beyond its gravitational characteristics, a uniform spherical shell also possesses interesting mechanical properties, notably its moment of inertia. The moment of inertia describes an object's resistance to changes in its rotation. For a uniform spherical shell, the moment of inertia (I) about an axis passing through its center is:
I = (2/3)mr²
where 'm' is the mass and 'r' is the radius of the shell. This equation indicates that the moment of inertia is proportional to both the mass and the square of the radius. This is crucial in understanding its rotational behavior under applied torques. A larger mass or radius leads to greater resistance to rotational acceleration.
Applications and Further Considerations
The theoretical properties of a uniform spherical shell have practical applications in various fields:
- Astrophysics: The shell theorem is instrumental in modeling the gravitational fields of planets and stars. The simplified calculations enabled by understanding this concept are indispensable in analyzing orbital mechanics and planetary formation.
- Nuclear Physics: The zero gravitational field inside a shell provides insights into certain theoretical nuclear models and their gravitational implications, although the dominant forces within an atomic nucleus are not gravitational.
- Theoretical Physics: The spherical shell serves as a fundamental model for studying more complex gravitational systems. Its simple geometry allows for analytic solutions, providing a stepping stone to tackle more intricate problems.
- Engineering: Though less direct, understanding moment of inertia calculations for spherical shells contributes to various design processes where rotational dynamics are important.
Beyond the perfect uniform shell, we can extend this understanding to consider real-world applications. While perfect uniformity is an idealization, many celestial bodies and manufactured objects approximate the behavior of a spherical shell. Understanding deviations from perfect uniformity allows for more accurate modeling of their gravitational and mechanical characteristics. Factors like non-uniform density distribution, irregularities in the shape, and variations in material properties contribute significantly to the real-world behavior. These deviations need to be taken into account for accurate predictions.
Conclusion
The uniform spherical shell, despite its apparent simplicity, holds a wealth of physical significance. Its unique gravitational properties—a zero field inside and a point-mass equivalent outside—make it a powerful tool for theoretical analysis and practical application in astrophysics and related fields. The understanding of its mechanical properties, particularly its moment of inertia, further enhances its utility in various engineering and scientific endeavors. While the ideal uniform spherical shell is a theoretical construct, its analysis provides a strong foundational understanding for more complex and realistic scenarios. Its study highlights the elegant power of symmetry in simplifying complex physical systems, laying the groundwork for a deeper understanding of the universe around us. Further research into refining the models that incorporate deviations from ideal uniformity will continue to enhance the accuracy and predictive power of these fundamental concepts.
Latest Posts
Latest Posts
-
A Carbohydrate That Makes Up The Cell Walls Of Plants
Apr 01, 2025
-
Cell Organelles Found Only In Plants
Apr 01, 2025
-
One Billion Is How Many Crores
Apr 01, 2025
-
What Is The Oxidation State Of N In Nh4
Apr 01, 2025
-
Which Of The Following Compounds Is Are Chiral
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about A Uniform Spherical Shell Of Mass M . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
