98 As Product Of Prime Factors
News Leon
Mar 26, 2025 · 5 min read
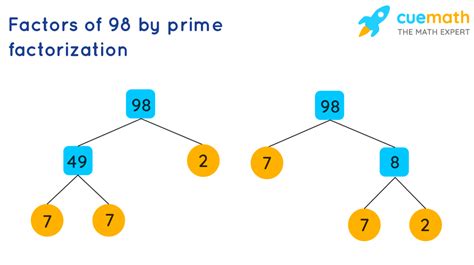
Table of Contents
98 as a Product of Prime Factors: A Deep Dive into Prime Factorization
Prime factorization, the process of breaking down a number into its prime number components, is a fundamental concept in number theory. It underpins many mathematical operations and algorithms, and understanding it provides a deeper appreciation for the structure of numbers. This article delves into the prime factorization of 98, exploring the process, its significance, and extending the concepts to broader applications.
Understanding Prime Numbers and Prime Factorization
Before we tackle the factorization of 98, let's refresh our understanding of key terms:
-
Prime Number: A prime number is a natural number greater than 1 that is not a product of two smaller natural numbers. In other words, its only divisors are 1 and itself. Examples include 2, 3, 5, 7, 11, and so on.
-
Composite Number: A composite number is a positive integer that has at least one divisor other than 1 and itself. All composite numbers can be expressed as a product of prime numbers.
-
Prime Factorization: This is the process of expressing a composite number as a product of its prime factors. This representation is unique for every composite number, ignoring the order of the factors. This uniqueness is guaranteed by the Fundamental Theorem of Arithmetic.
Finding the Prime Factors of 98
Now, let's find the prime factorization of 98. We can use a factor tree or repeated division by prime numbers to achieve this.
Method 1: Factor Tree
A factor tree visually represents the factorization process. We start by finding any two factors of 98. A convenient pair is 2 and 49:
98
/ \
2 49
/ \
7 7
We see that 2 is a prime number. 49, however, is not prime; it's 7 x 7. Since 7 is also a prime number, we have reached the end of our factorization. Therefore, the prime factorization of 98 is 2 x 7 x 7, or 2 x 7².
Method 2: Repeated Division
Alternatively, we can repeatedly divide 98 by prime numbers until we reach 1.
- Divide 98 by 2 (the smallest prime number): 98 / 2 = 49
- Divide 49 by 7 (the next prime number): 49 / 7 = 7
- Divide 7 by 7: 7 / 7 = 1
We have used the prime numbers 2 and 7 repeatedly to arrive at 1. Therefore, the prime factorization of 98 is 2 x 7 x 7 or 2 x 7².
The Significance of Prime Factorization
The prime factorization of a number isn't just a mathematical exercise; it has significant applications in various areas:
-
Cryptography: Prime numbers form the basis of many modern encryption algorithms, such as RSA encryption. The difficulty of factoring large numbers into their prime components is what makes these algorithms secure.
-
Number Theory: Prime factorization is a cornerstone of number theory, providing insights into the properties and relationships between numbers. It helps in solving Diophantine equations and other complex mathematical problems.
-
Computer Science: Algorithms for prime factorization are actively researched and improved. Efficient factorization algorithms are crucial for various computational tasks.
-
Modular Arithmetic: Prime factorization plays a crucial role in modular arithmetic, which has applications in cryptography and coding theory.
Extending the Concept: Larger Numbers and Algorithms
While the prime factorization of 98 is straightforward, factoring larger numbers can be significantly more challenging. For very large composite numbers, finding the prime factors becomes computationally intensive. This is why it's so important in cryptography.
Several algorithms exist for prime factorization, each with its strengths and weaknesses:
-
Trial Division: This is the simplest method, but it becomes extremely inefficient for large numbers. It involves testing divisibility by each prime number sequentially.
-
Sieve of Eratosthenes: This algorithm efficiently generates a list of prime numbers up to a specified limit, which can then be used for trial division.
-
Pollard's Rho Algorithm: This is a probabilistic algorithm, meaning it doesn't guarantee finding a factor but has a high probability of success. It's significantly faster than trial division for large numbers.
-
General Number Field Sieve (GNFS): This is the most efficient known algorithm for factoring very large numbers and is used to break certain cryptographic systems.
Practical Applications Beyond Cryptography
Beyond cryptography, the principles of prime factorization have practical applications in:
-
Simplifying Fractions: Finding the prime factors of the numerator and denominator allows for the simplification of fractions to their lowest terms. For example, 98/14 can be simplified by factoring 98 as 2 x 7² and 14 as 2 x 7.
-
Least Common Multiple (LCM) and Greatest Common Divisor (GCD): Prime factorization is essential for efficiently calculating the LCM and GCD of two or more numbers. The LCM is the smallest number divisible by all the given numbers, and the GCD is the largest number that divides all the given numbers.
Advanced Concepts and Related Topics
The concept of prime factorization extends to more advanced mathematical topics such as:
-
Unique Factorization Domain (UFD): The Fundamental Theorem of Arithmetic states that every integer greater than 1 can be uniquely factored into primes. This concept generalizes to other algebraic structures called unique factorization domains.
-
Algebraic Number Theory: This branch of mathematics studies algebraic numbers and their properties, often utilizing prime factorization in various contexts.
Conclusion: The Enduring Importance of Prime Factorization
The seemingly simple concept of prime factorization underlies a vast array of mathematical and computational applications. From the security of our online transactions to the elegant structure of number theory, prime numbers and their factorization continue to be a source of fascination and profound importance in mathematics and computer science. While factoring small numbers like 98 is straightforward, understanding the underlying principles and the algorithms used for larger numbers provides a deep appreciation of this fundamental concept. The journey from a simple factor tree to sophisticated algorithms highlights the power and beauty of prime factorization. The seemingly simple task of breaking down 98 into its prime factors – 2 and 7 – serves as a gateway to a vast and fascinating world of mathematical exploration.
Latest Posts
Latest Posts
-
Diagram Of A Simple Reflex Arc
Mar 29, 2025
-
Is Wax Melting A Chemical Change
Mar 29, 2025
-
How Many Nitrogen Bases Make Up A Codon
Mar 29, 2025
-
What Is The Electron Configuration Of Br
Mar 29, 2025
-
76 8 Of What Number Is 40 32
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about 98 As Product Of Prime Factors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
