3x Y 2 6x 2y 4
News Leon
Apr 06, 2025 · 5 min read
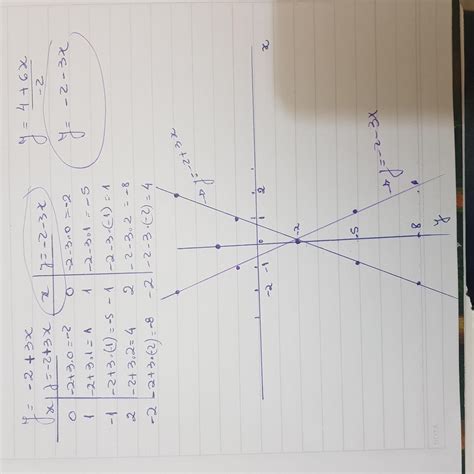
Table of Contents
Deconstructing the Mathematical Expression: 3x + 2 = 6x + 2y + 4
This seemingly simple algebraic equation, 3x + 2 = 6x + 2y + 4, presents a fascinating opportunity to delve into the world of mathematical problem-solving and explore various approaches to finding solutions. While it might appear straightforward at first glance, the presence of two variables (x and y) introduces an element of complexity, requiring a deeper understanding of algebraic manipulation and the concept of solution sets. This article will comprehensively explore this equation, examining its structure, potential solutions, and the broader mathematical principles it embodies.
Understanding the Equation's Structure
The equation 3x + 2 = 6x + 2y + 4 is a linear equation in two variables. This means it represents a straight line when graphed on a Cartesian coordinate system. The presence of two variables signifies that there's not a single unique solution, but rather an infinite number of solutions that satisfy the equation. These solutions form the line itself.
To understand the equation better, let's break it down:
- 3x: This term represents three times the value of the variable 'x'.
- 2: This is a constant term.
- 6x: This term represents six times the value of the variable 'x'.
- 2y: This term represents two times the value of the variable 'y'.
- 4: This is another constant term.
The equation states that the expression on the left-hand side (3x + 2) is equal to the expression on the right-hand side (6x + 2y + 4). Our goal is to find the values of 'x' and 'y' that make this statement true.
Solving for One Variable in Terms of the Other
Since we have two variables, we cannot solve for definitive numerical values for x and y without additional information (like a second independent equation). However, we can express one variable in terms of the other. This will provide a relationship between x and y that holds true for all solutions to the original equation.
Let's rearrange the equation to solve for 'y' in terms of 'x':
- Subtract 3x from both sides: 2 = 3x + 2y + 4
- Subtract 4 from both sides: -2 = 3x + 2y
- Subtract 3x from both sides: -3x - 2 = 2y
- Divide both sides by 2: y = (-3x - 2) / 2
- Simplify: y = -3x/2 - 1
This equation, y = -3x/2 - 1, tells us that for any given value of 'x', we can calculate the corresponding value of 'y' that satisfies the original equation. This representation is extremely useful for graphing the equation and understanding the solution set.
Similarly, we can solve for 'x' in terms of 'y':
- Subtract 2 from both sides: 3x = 6x + 2y + 2
- Subtract 6x from both sides: -3x = 2y + 2
- Divide both sides by -3: x = (-2y - 2) / 3
- Simplify: x = (-2/3)y - (2/3)
This provides another perspective on the relationship between x and y, enabling us to find x given a value for y.
Graphing the Equation
The equation, when graphed, will appear as a straight line. This is because it's a linear equation. The equation y = -3x/2 - 1 (or its equivalent x = (-2/3)y - (2/3)) is in the slope-intercept form (y = mx + b), where 'm' represents the slope and 'b' represents the y-intercept.
In our case:
- Slope (m) = -3/2: This indicates that for every two units moved to the right along the x-axis, the line moves three units down along the y-axis. The negative slope means the line is decreasing.
- Y-intercept (b) = -1: This means the line intersects the y-axis at the point (0, -1).
By plotting the y-intercept and using the slope to find additional points, you can accurately graph the line representing the infinite solutions to the equation. Every point on this line (x,y) will satisfy the original equation 3x + 2 = 6x + 2y + 4.
Exploring Specific Solution Sets
While there is no single solution, we can find specific pairs of (x,y) that satisfy the equation. Let's explore a few examples:
- If x = 0: Substituting x = 0 into y = -3x/2 - 1, we get y = -1. Therefore, (0, -1) is a solution.
- If x = 2: Substituting x = 2 into y = -3x/2 - 1, we get y = -4. Therefore, (2, -4) is a solution.
- If y = 0: Substituting y = 0 into x = (-2/3)y - (2/3), we get x = -2/3. Therefore, (-2/3, 0) is a solution.
These are just a few examples; infinitely many such pairs exist along the line defined by the equation.
Applications and Further Exploration
Understanding and solving linear equations like 3x + 2 = 6x + 2y + 4 is fundamental to many areas of mathematics and its applications. These concepts are crucial in:
- Linear Algebra: Forms the basis for understanding systems of linear equations and matrices.
- Calculus: Used in finding derivatives and integrals of linear functions.
- Computer Graphics: Essential for representing lines and shapes in computer-generated images.
- Physics and Engineering: Used extensively in modeling physical systems and solving problems related to motion, forces, and energy.
- Economics: Used in constructing and analyzing economic models.
This seemingly simple equation opens the door to a vast world of mathematical concepts and applications. By exploring its structure, solving for variables, graphing the solutions, and understanding its implications, we gain a deeper appreciation for the power and elegance of algebra. The ability to manipulate equations, interpret results, and visualize solutions is a crucial skill in numerous fields, highlighting the practical significance of mastering fundamental algebraic techniques. Further exploration could involve examining systems of equations that might include 3x + 2 = 6x + 2y + 4 as one of its components, leading to unique solutions where both x and y are definitively determined. This underlines the importance of context and the need for sufficient information to completely resolve a system of equations.
Latest Posts
Latest Posts
-
How Many Significant Figures Are In 0 020
Apr 07, 2025
-
3 Ways To Increase The Strength Of An Electromagnet
Apr 07, 2025
-
How Many Neutrons Are In An Atom Of Magnesium 25
Apr 07, 2025
-
Which Of The Following Is The Correct Formula
Apr 07, 2025
-
What Is Between 1 4 And 1 8
Apr 07, 2025
Related Post
Thank you for visiting our website which covers about 3x Y 2 6x 2y 4 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.