30 As A Product Of Prime Factors
News Leon
Mar 28, 2025 · 5 min read
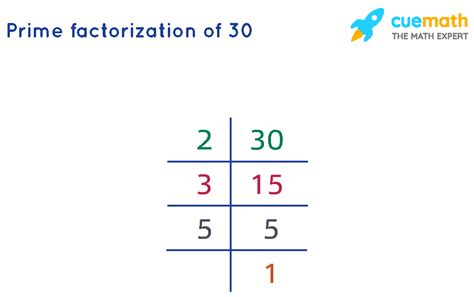
Table of Contents
30 as a Product of Prime Factors: A Deep Dive into Prime Factorization
The seemingly simple number 30 holds a fascinating secret within its numerical structure: its prime factorization. Understanding how to break down a number into its prime factors is a fundamental concept in number theory, with applications ranging from cryptography to efficient algorithm design. This article delves deep into the prime factorization of 30, exploring the process, its significance, and related mathematical concepts. We'll also explore the practical applications and implications of understanding prime factorization.
What is Prime Factorization?
Before we dissect 30, let's clarify the core concept. Prime factorization (also known as prime decomposition) is the process of finding the prime numbers that, when multiplied together, result in the original number. A prime number is a whole number greater than 1 that has only two divisors: 1 and itself. Examples include 2, 3, 5, 7, 11, and so on. Numbers that are not prime are called composite numbers.
The Fundamental Theorem of Arithmetic guarantees that every composite number can be expressed as a unique product of prime numbers (ignoring the order of factors). This uniqueness is crucial in various mathematical operations and proofs.
Finding the Prime Factors of 30
Now, let's find the prime factors of 30. We can use a factor tree to visualize the process:
30
/ \
2 15
/ \
3 5
Starting with 30, we identify a pair of factors. The smallest prime factor of 30 is 2 (since 30 is an even number), so we branch out to 2 and 15. 15 is not prime (it's divisible by 3 and 5), so we continue breaking down 15 into its prime factors, 3 and 5. Both 3 and 5 are prime numbers.
Therefore, the prime factorization of 30 is 2 x 3 x 5.
We can also express this using exponents if there are repeated prime factors. For example, the prime factorization of 12 is 2 x 2 x 3, which can be written as 2² x 3.
The Significance of Prime Factorization
The seemingly simple process of prime factorization has profound implications across various fields of mathematics and computer science:
1. Greatest Common Divisor (GCD) and Least Common Multiple (LCM)
Prime factorization is essential for efficiently calculating the greatest common divisor (GCD) and the least common multiple (LCM) of two or more numbers.
-
GCD: The GCD is the largest number that divides two or more numbers without leaving a remainder. Finding the GCD using prime factorization involves identifying the common prime factors and their lowest powers.
-
LCM: The LCM is the smallest number that is a multiple of two or more numbers. Finding the LCM using prime factorization involves identifying all the prime factors and their highest powers.
For example, let's find the GCD and LCM of 30 and 42:
-
Prime factorization of 30: 2 x 3 x 5
-
Prime factorization of 42: 2 x 3 x 7
-
GCD(30, 42): The common prime factors are 2 and 3. The lowest power of 2 is 2¹, and the lowest power of 3 is 3¹. Therefore, GCD(30, 42) = 2 x 3 = 6.
-
LCM(30, 42): The prime factors are 2, 3, 5, and 7. The highest power of 2 is 2¹, the highest power of 3 is 3¹, the highest power of 5 is 5¹, and the highest power of 7 is 7¹. Therefore, LCM(30, 42) = 2 x 3 x 5 x 7 = 210.
2. Cryptography
Prime factorization plays a crucial role in modern cryptography, particularly in public-key cryptography systems like RSA. RSA relies on the difficulty of factoring very large numbers into their prime factors. The security of RSA depends on the computational infeasibility of factoring the product of two large prime numbers.
3. Modular Arithmetic
Prime factorization is fundamental in modular arithmetic, a system of arithmetic for integers where numbers "wrap around" upon reaching a certain value (the modulus). Modular arithmetic is crucial in cryptography and computer science.
4. Algorithm Efficiency
Many algorithms in computer science rely on prime factorization for efficient computation. For example, algorithms related to finding the GCD and LCM are significantly faster when using prime factorization.
Advanced Concepts Related to Prime Factorization
1. The Sieve of Eratosthenes
The Sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to a specified integer. It's an efficient method for generating a list of prime numbers, useful for various applications.
2. Distribution of Prime Numbers
The distribution of prime numbers is a complex and fascinating area of number theory. The Prime Number Theorem provides an approximation for the number of primes less than a given number.
3. Primality Testing
Determining whether a given number is prime is crucial for prime factorization and other applications. Sophisticated primality tests, like the Miller-Rabin test, are used to efficiently determine the primality of large numbers.
Practical Applications of Prime Factorization
Beyond the theoretical aspects, prime factorization has numerous practical applications:
- Simplifying Fractions: Prime factorization helps simplify fractions by identifying common factors in the numerator and denominator.
- Solving Equations: Understanding prime factorization can aid in solving certain types of algebraic equations.
- Scheduling and Planning: Concepts like LCM are used in scheduling tasks and events that need to occur at regular intervals.
- Coding and Computer Science: Prime factorization underlies several algorithms and data structures used in computer programming.
Conclusion
The prime factorization of 30, 2 x 3 x 5, is more than just a simple mathematical decomposition. It represents a gateway to understanding fundamental concepts in number theory and their far-reaching implications. From cryptography and algorithm design to the efficient calculation of GCDs and LCMs, the ability to factor numbers into their prime components is a cornerstone of many mathematical and computational processes. By delving into this seemingly simple concept, we unlock a deeper appreciation for the elegance and power of prime numbers and their role in the world of mathematics and beyond. Further exploration of these concepts will undoubtedly lead to a more profound understanding of the intricate structure of numbers and their diverse applications. The simplicity of the prime factorization of 30 belies the profound impact this concept has on various fields, highlighting the beauty and practical significance of fundamental mathematical principles.
Latest Posts
Latest Posts
-
Who Is The Father Of Bio
Mar 31, 2025
-
Which Of The Following Is True About Genes
Mar 31, 2025
-
What Animal Has The Largest Breasts
Mar 31, 2025
-
Which Two Bonds Are Most Similar In Polarity
Mar 31, 2025
-
13 With 3 Repeating As A Fraction
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about 30 As A Product Of Prime Factors . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
