Y Varies Inversely As The Square Of X
News Leon
Apr 07, 2025 · 6 min read
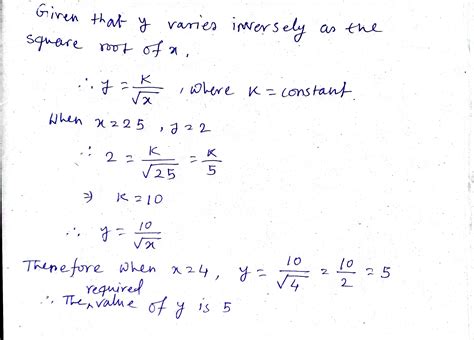
Table of Contents
Y Varies Inversely as the Square of X: A Comprehensive Guide
Understanding inverse relationships is crucial in various fields, from physics and engineering to economics and social sciences. This article delves into the specific case where one variable, y, varies inversely as the square of another variable, x. We'll explore the mathematical representation, real-world applications, graphing techniques, and problem-solving strategies associated with this important concept.
Understanding Inverse Variation
Before diving into the specifics of inverse square variation, let's establish a foundation in inverse relationships. Inverse variation describes a relationship between two variables where an increase in one variable leads to a proportional decrease in the other, and vice versa. The general form is:
y = k/x
where:
- y and x are the variables.
- k is the constant of variation. This constant represents the strength of the inverse relationship.
This means that the product of x and y always equals the constant k. If you double x, y will be halved; if you triple x, y will be reduced to one-third its original value, and so on.
Y Varies Inversely as the Square of X: The Mathematical Representation
Now, let's focus on the specific scenario where y varies inversely as the square of x. The mathematical representation of this relationship is:
y = k/x²
This equation signifies that y is inversely proportional to the square of x. A change in x will have a more pronounced effect on y than in a simple inverse relationship. For instance, doubling x will result in y becoming one-fourth of its original value (because 2² = 4). Tripling x will make y one-ninth of its original value (because 3² = 9).
Key Differences from Simple Inverse Variation:
The inverse square relationship differs significantly from a simple inverse relationship because of the squared term. This leads to a steeper decline in y as x increases. Consider the following examples:
- Simple Inverse: If y = k/x and x doubles, y halves.
- Inverse Square: If y = k/x² and x doubles, y becomes one-fourth its original value.
This amplified effect is crucial in understanding many physical phenomena.
Finding the Constant of Variation (k)
To fully define the inverse square relationship, we need to determine the constant of variation, k. This is done by using a known pair of values for x and y. Let's say we know that when x = 2, y = 8. Substituting these values into the equation:
8 = k/2²
Solving for k:
k = 8 * 4 = 32
Therefore, the specific inverse square relationship is:
y = 32/x²
This equation allows us to calculate y for any given value of x, or vice versa.
Real-World Applications of Inverse Square Relationships
Inverse square relationships are prevalent in many aspects of the natural world and various scientific disciplines. Some notable examples include:
1. Physics: Gravitational Force and Intensity of Light
-
Newton's Law of Universal Gravitation: The gravitational force between two objects is inversely proportional to the square of the distance between their centers. This means that the further apart two objects are, the weaker the gravitational force between them becomes, and this weakening is not linear but rather follows an inverse square law.
-
Intensity of Light: The intensity of light from a point source is inversely proportional to the square of the distance from the source. Moving twice as far from a light bulb results in a light intensity that is only one-fourth as bright.
2. Engineering: Signal Strength and Sound Intensity
-
Radio Waves and Other Electromagnetic Waves: The strength of a radio signal diminishes according to the inverse square law. The further you are from the transmitter, the weaker the signal.
-
Sound Intensity: The intensity of sound decreases with the square of the distance from the source. This is why sounds seem fainter the further you are from their source.
3. Other Fields:
-
Economics: Certain economic models utilize inverse square relationships to model phenomena like the spread of influence or the impact of marketing campaigns.
-
Social Sciences: The spread of information or the influence of social trends might, in some simplified models, follow an inverse square relationship.
Graphing Inverse Square Relationships
Graphing an inverse square relationship provides a visual representation of how y changes with x. The graph will always be a hyperbola.
-
Key Characteristics: The graph will be located in the first and second quadrants (since x² is always positive and k is usually positive, y will always be positive). The curve approaches, but never touches, the x-axis and the y-axis. As x approaches infinity, y approaches zero. As x approaches zero, y approaches infinity.
-
Impact of the Constant k: The value of k determines the "steepness" of the hyperbola. A larger value of k results in a hyperbola that is further from the axes.
Problem Solving with Inverse Square Relationships
Solving problems involving inverse square relationships involves applying the formula y = k/x² and using algebraic techniques. Here's a step-by-step approach:
- Identify the variables: Determine which variable represents y and which represents x.
- Find the constant of variation (k): If given a pair of values for x and y, substitute these values into the equation to solve for k.
- Write the equation: Write the complete equation with the calculated value of k.
- Solve for the unknown: Use the equation to solve for either x or y based on the problem's requirements.
Example Problem:
The intensity (I) of light varies inversely as the square of the distance (d) from the source. If the intensity is 16 lumens at a distance of 2 meters, what is the intensity at a distance of 4 meters?
- Variables: I = intensity, d = distance.
- Find k: 16 = k/2² => k = 64
- Equation: I = 64/d²
- Solve: At d = 4 meters, I = 64/4² = 4 lumens.
Variations and Extensions
The basic inverse square relationship can be modified and extended to include additional factors. For example, you could have a relationship where y varies inversely as the square of x and directly as z, expressed as:
y = kz²/x²
In such cases, solving problems involves similar steps: identifying variables, finding the constant of variation (which now depends on both z and x), writing the equation, and solving for the unknowns.
Conclusion
Understanding the concept of "y varies inversely as the square of x" is fundamental to comprehending many physical and other scientific phenomena. By mastering the mathematical representation, applications, graphing techniques, and problem-solving strategies associated with this concept, you'll be equipped to analyze and interpret a wide range of real-world situations and solve related problems effectively. This comprehensive understanding of inverse square relationships opens doors to deeper comprehension in various scientific and engineering disciplines. Remember to always carefully identify the variables and constant of proportionality to accurately model and solve problems involving this important relationship.
Latest Posts
Latest Posts
-
Is Gallium Liquid At Room Temperature
Apr 09, 2025
-
How Many Total Electrons Are In A Fe2 Ion
Apr 09, 2025
-
Which Of The Following Does Not Occur In The Mitochondria
Apr 09, 2025
-
Why Is Ice Melting Not A Chemical Change
Apr 09, 2025
-
Which Of The Following Is Not A Solvency Ratio
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Y Varies Inversely As The Square Of X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.