X To The Power Of X Derivative
News Leon
Apr 03, 2025 · 6 min read
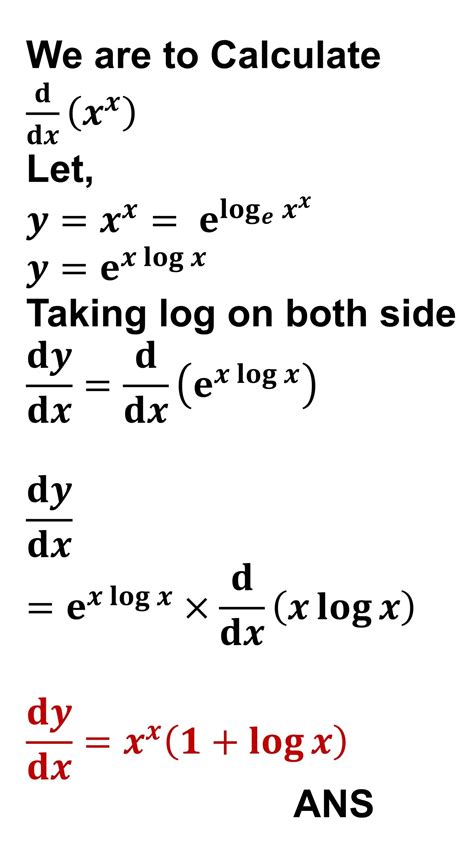
Table of Contents
The Derivative of x<sup>x</sup>: A Comprehensive Guide
The derivative of x<sup>x</sup> is a fascinating problem that elegantly demonstrates the power and flexibility of calculus. Unlike simpler power functions, where the power is a constant, this function involves a variable base and a variable exponent. This necessitates the use of logarithmic differentiation, a powerful technique for handling complex functions. Let's explore this in detail.
Understanding the Challenge: Why Simple Power Rules Fail
Before diving into the solution, it's crucial to understand why standard differentiation rules, like the power rule (d/dx(x<sup>n</sup>) = nx<sup>n-1</sup>), are insufficient here. The power rule applies when the exponent is a constant. In x<sup>x</sup>, however, both the base and the exponent are variables, rendering the power rule inapplicable. This necessitates a more sophisticated approach.
Employing Logarithmic Differentiation: The Key to the Solution
Logarithmic differentiation is a technique that simplifies the differentiation of complex functions, especially those involving products, quotients, and variable exponents. It leverages the properties of logarithms to transform the function into a more manageable form before applying differentiation.
Here's how we apply logarithmic differentiation to find the derivative of x<sup>x</sup>:
-
Introduce the Natural Logarithm: Start by taking the natural logarithm (ln) of both sides of the equation y = x<sup>x</sup>:
ln(y) = ln(x<sup>x</sup>)
-
Utilize Logarithmic Properties: Using the power rule of logarithms (ln(a<sup>b</sup>) = b ln(a)), simplify the right-hand side:
ln(y) = x ln(x)
-
Implicit Differentiation: Now, differentiate both sides of the equation with respect to x, remembering to apply the chain rule on the left-hand side and the product rule on the right-hand side:
(1/y) * (dy/dx) = ln(x) + x * (1/x)
-
Simplify and Solve for dy/dx: Simplify the equation and solve for dy/dx, which represents the derivative of y = x<sup>x</sup> with respect to x:
(1/y) * (dy/dx) = ln(x) + 1
dy/dx = y * (ln(x) + 1)
-
Substitute Back: Finally, substitute the original expression for y (y = x<sup>x</sup>) back into the equation:
dy/dx = x<sup>x</sup>(ln(x) + 1)
Therefore, the derivative of x<sup>x</sup> is x<sup>x</sup>(ln(x) + 1).
A Step-by-Step Breakdown with Detailed Explanations
Let's dissect each step of the logarithmic differentiation process to ensure complete understanding:
Step 1: Taking the Natural Logarithm
Taking the natural logarithm of both sides allows us to utilize the properties of logarithms to simplify the expression. The natural logarithm, denoted as ln, is the logarithm to the base e (Euler's number, approximately 2.718). This choice isn't arbitrary; the natural logarithm simplifies calculations involving exponential functions and their derivatives.
Step 2: Applying the Power Rule of Logarithms
The power rule of logarithms states that ln(a<sup>b</sup>) = b ln(a). Applying this rule to ln(x<sup>x</sup>) allows us to bring the exponent (x) down as a coefficient, transforming the expression into a simpler form that is more amenable to differentiation.
Step 3: Implicit Differentiation and the Chain Rule
Implicit differentiation is a technique used to differentiate equations where y is not explicitly defined as a function of x. The chain rule is essential here because we are differentiating ln(y) with respect to x. The chain rule states that d/dx[f(g(x))] = f'(g(x)) * g'(x). In this case, f(y) = ln(y), and g(x) = x<sup>x</sup>. Therefore, the derivative of ln(y) with respect to x is (1/y) * (dy/dx). The product rule is also applied on the right hand side, d/dx[uv] = u dv/dx + v du/dx, with u = x and v = ln(x).
Step 4: Solving for dy/dx
Solving for dy/dx involves simple algebraic manipulation. We isolate dy/dx by multiplying both sides of the equation by y.
Step 5: Back-Substitution
The final step is to substitute the original expression for y (y = x<sup>x</sup>) back into the equation to express the derivative solely in terms of x.
Applications and Extensions
The derivative of x<sup>x</sup>, x<sup>x</sup>(ln(x) + 1), has applications in various fields, including:
-
Optimization Problems: Finding maxima and minima of functions involving x<sup>x</sup> often requires finding the derivative and setting it to zero.
-
Calculus of Variations: This derivative is used in problems dealing with functional optimization.
-
Numerical Analysis: The derivative can be used in numerical methods to approximate the function's behavior.
-
Modeling in Science and Engineering: x<sup>x</sup> can appear in models describing exponential growth with a variable exponent, so its derivative is crucial for analyzing the rate of change.
Exploring Related Derivatives: Generalizing the Technique
The technique of logarithmic differentiation can be extended to other functions of a similar form, such as (f(x))<sup>g(x)</sup>, where f(x) and g(x) are differentiable functions. The general approach would follow the same steps, but the specific derivative will depend on the form of f(x) and g(x). For instance, consider finding the derivative of (sin x)<sup>x</sup>. We’d follow the same steps, using the chain rule and product rule as needed during implicit differentiation.
The key takeaway is that logarithmic differentiation offers a powerful and elegant approach to handling the derivatives of complex functions that defy simpler differentiation techniques.
Addressing Potential Pitfalls and Common Mistakes
Several points warrant attention to avoid common mistakes:
-
Forgetting the Chain Rule: The chain rule is crucial in step 3. Failure to apply the chain rule will lead to an incorrect derivative.
-
Incorrect Application of Logarithmic Rules: Ensure that you correctly apply the logarithmic rules. Common mistakes include incorrectly using the power rule or sum/difference rules of logarithms.
-
Algebraic Errors: Carefully execute the algebraic manipulations involved in solving for dy/dx. Simple algebraic mistakes can propagate and lead to incorrect results.
-
Failing to Substitute Back: Remember to substitute back the original expression for y after obtaining the derivative in terms of y and dy/dx.
By carefully following the steps and paying close attention to these potential pitfalls, you can accurately calculate the derivative of x<sup>x</sup> and similar complex functions.
Conclusion: Mastering Logarithmic Differentiation
The derivative of x<sup>x</sup>, x<sup>x</sup>(ln(x) + 1), is a powerful illustration of the utility of logarithmic differentiation in calculus. This technique transcends the limitations of simpler differentiation rules, providing a versatile tool for handling a wide range of complex functions. By understanding the underlying principles and applying the steps methodically, you'll develop a crucial skill applicable in numerous advanced mathematical and scientific contexts. Mastering logarithmic differentiation is not merely about obtaining an answer; it's about acquiring a problem-solving approach applicable far beyond this specific function.
Latest Posts
Latest Posts
-
Any Computer Parts That You Can Actually Touch
Apr 04, 2025
-
Which Of The Following Is Hydrophobic
Apr 04, 2025
-
Do Prokaryotes Have A Membrane Bound Organelles
Apr 04, 2025
-
Why Was A Stain Added To The Cheek Cells
Apr 04, 2025
-
What Is A Group Of Tissues That Work Together Called
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about X To The Power Of X Derivative . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
