X 3 X 3 X 3
News Leon
May 04, 2025 · 5 min read
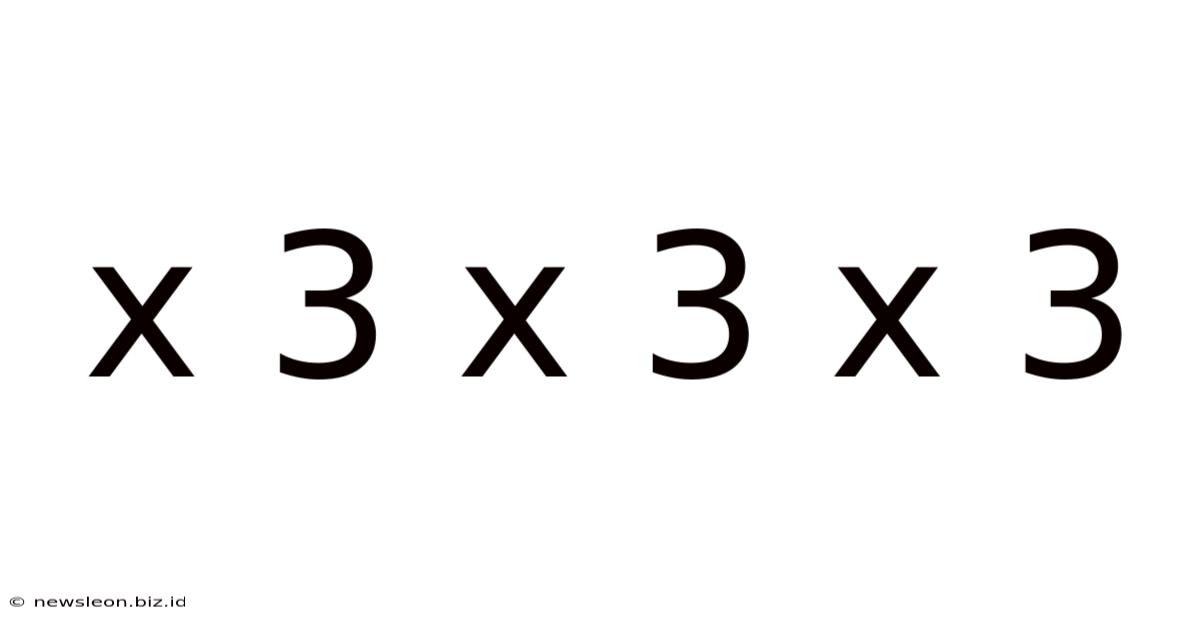
Table of Contents
Decoding 3 x 3 x 3: Exploring the Multifaceted Nature of a Simple Equation
The seemingly simple equation, 3 x 3 x 3, offers a surprising depth of exploration across various fields. While the mathematical answer is straightforward (27), delving deeper reveals connections to geometry, computer science, problem-solving, and even philosophy. This article explores the multifaceted nature of 3 x 3 x 3, uncovering its hidden layers and demonstrating its significance beyond a basic arithmetic calculation.
The Mathematical Foundation: 3 x 3 x 3 = 27
At its core, 3 x 3 x 3 is a simple multiplication problem. It represents repeated multiplication: three multiplied by itself three times. The solution, 27, is a fundamental building block in numerous mathematical operations and concepts. This seemingly basic calculation forms the foundation for more complex mathematical structures and is crucial in understanding exponential growth, volume calculations, and combinatorial analysis. Understanding this fundamental calculation is key to grasping more advanced mathematical principles.
Beyond Simple Multiplication: Exploring Exponential Growth
The equation 3 x 3 x 3 can be expressed as 3<sup>3</sup>, illustrating the concept of exponentiation. This signifies exponential growth, a crucial concept in numerous fields. Think of compound interest, population growth, or the spread of infectious diseases – all modeled using exponential functions. The equation acts as a miniature illustration of how quickly values can increase when repeatedly multiplied by a base number greater than one. Understanding this exponential growth is key to predicting future trends and making informed decisions in various aspects of life.
Geometric Interpretations: Cubes and Spatial Reasoning
The equation 3 x 3 x 3 has a direct visual representation in geometry. It defines the volume of a cube with sides of length 3 units. This connection highlights the relationship between abstract mathematical equations and real-world objects, strengthening spatial reasoning skills. Visualizing this cube helps connect the abstract concept of multiplication with a tangible, three-dimensional form. It also paves the way for understanding more complex geometric shapes and volume calculations.
Applications in Computer Science: Arrays, Data Structures, and Algorithms
In computer science, the 3 x 3 x 3 structure resonates with the concept of three-dimensional arrays. These arrays are data structures used to organize data in a grid-like format, often used to represent images, matrices, or game environments. A 3 x 3 x 3 array would be a cube of data, with each element accessible through its three-dimensional coordinates. This structure is essential for algorithms involved in image processing, computer graphics, and simulations.
The Rubik's Cube: A Tangible Representation of Complexity
The iconic Rubik's Cube, with its 3 x 3 x 3 arrangement of smaller cubes, provides a fascinating example of the equation's impact. Solving a Rubik's Cube involves manipulating these smaller cubes to restore the overall structure. This complex puzzle illustrates how a seemingly simple structure can lead to immense computational challenges. Algorithms to solve a Rubik's cube leverage the underlying 3 x 3 x 3 structure, demonstrating the application of mathematical concepts in real-world problem-solving.
Problem-Solving and Logical Reasoning: Breaking Down Complexities
The equation 3 x 3 x 3, while simple in its execution, can be used as a foundation for developing problem-solving skills. It can be used to introduce learners to algebraic thinking and the importance of order of operations. Presenting similar problems with different numbers helps in pattern recognition and developing strategies for tackling more complex mathematical problems.
Beyond Arithmetic: Connecting to Logic Puzzles and Games
The structure inherent in 3 x 3 x 3 can inspire various logic puzzles and games. Consider Sudoku, where numbers are strategically placed within a 9 x 9 grid, or tic-tac-toe, played on a 3 x 3 board. These games subtly use the underlying principles of structure and pattern recognition, sharpening logical reasoning skills and enhancing cognitive abilities.
Philosophical Implications: Simplicity and Complexity
The seemingly simple equation, 3 x 3 x 3 = 27, embodies a deeper philosophical point – the relationship between simplicity and complexity. The simplicity of the equation contrasts with the complexity of its applications across different fields. This highlights the interconnectedness of seemingly disparate areas of knowledge and the potential for a single concept to have profound implications across various disciplines.
The Power of Simplicity: Foundations of Complex Systems
The equation's simplicity underscores the importance of foundational concepts in building more complex systems. It demonstrates how fundamental mathematical principles form the basis for advanced computations and intricate structures. This simple equation stands as a testament to the power of fundamental building blocks in shaping complex realities.
Conclusion: Unveiling the Hidden Depths of 3 x 3 x 3
While the answer to 3 x 3 x 3 is a simple 27, the journey of exploring its multifaceted nature unveils its profound significance across various disciplines. From the fundamentals of mathematical operations and exponential growth to the intricate workings of computer science, geometric visualizations, and problem-solving strategies, this equation demonstrates how a simple concept can have a remarkable impact on our understanding of the world. The exploration of 3 x 3 x 3 offers a powerful lesson – the hidden depths often lie beneath the surface of seemingly simple concepts, rewarding those who delve deeper with a richer understanding and appreciation. It serves as a reminder that even the simplest concepts can unlock vast possibilities when examined from different perspectives. Further investigation into related concepts such as prime factorization, modular arithmetic, and advanced geometric principles would further expand the understanding of the implications embedded within this seemingly simplistic equation. The inherent scalability of the 3 x 3 x 3 structure also allows for exploration of higher-dimensional equivalents, opening doors to even more complex applications and research areas. The study of this equation serves as a microcosm of the broader scientific process, encouraging curiosity, exploration, and a deeper appreciation for the interconnectedness of knowledge.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 X 3 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.