X 3 X 2 X 3
News Leon
May 04, 2025 · 5 min read
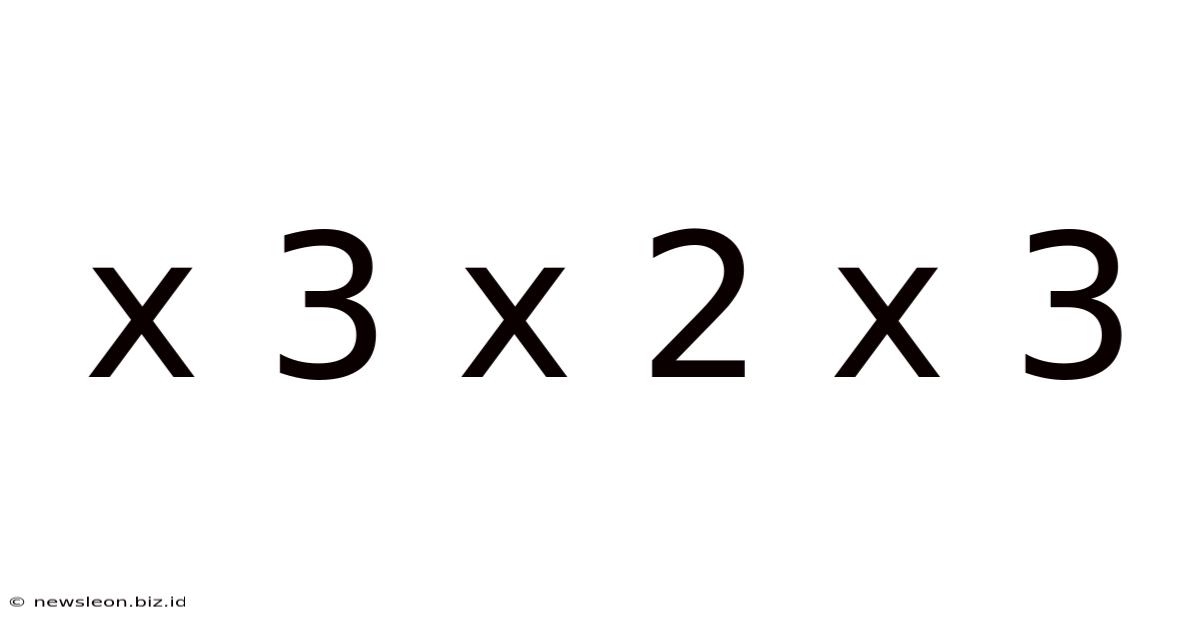
Table of Contents
Decoding the Mystery: A Deep Dive into x³ x² x³
The seemingly simple expression "x³ x² x³" holds a wealth of mathematical richness, extending far beyond its initial appearance. This article will explore this expression from multiple perspectives, examining its simplification, its applications in various mathematical contexts, and its implications within broader mathematical concepts. We will delve into the underlying principles of exponents, polynomial manipulation, and even touch upon the visual representations and real-world applications of this fundamental algebraic concept.
Understanding the Fundamentals: Exponents and their Properties
Before we tackle the complexities (or rather, the simplicity!) of x³ x² x³, let's solidify our understanding of exponents. An exponent, or power, indicates how many times a base number is multiplied by itself. In the expression x³, the 'x' is the base, and the '3' is the exponent, meaning x multiplied by itself three times (x * x * x).
Key Properties of Exponents:
- Multiplication of exponents with the same base: When multiplying terms with the same base, you add the exponents. This is the core principle we'll leverage to simplify our expression. For example, x² * x³ = x⁽²⁺³⁾ = x⁵.
- Division of exponents with the same base: When dividing terms with the same base, you subtract the exponents. For example, x⁵ / x² = x⁽⁵⁻²⁾ = x³.
- Power of a power: When raising a power to another power, you multiply the exponents. For instance, (x²)³ = x⁽²*³⁾ = x⁶.
- Exponent of 0: Any base raised to the power of 0 equals 1 (except for 0⁰, which is undefined). For example, x⁰ = 1.
- Exponent of 1: Any base raised to the power of 1 equals itself. For example, x¹ = x.
Simplifying x³ x² x³
Now, armed with our understanding of exponent properties, let's tackle the simplification of x³ x² x³:
x³ x² x³ = x⁽³⁺²⁺³⁾ = x⁸
This simplification is achieved by applying the rule for multiplying exponents with the same base. We add the exponents (3 + 2 + 3) to obtain the final simplified form, x⁸. This process demonstrates the elegance and efficiency of algebraic manipulation.
Expanding the Scope: Polynomials and Their Applications
Our expression, in its simplified form (x⁸), represents a monomial – a polynomial with only one term. However, the principles involved extend directly to more complex polynomial expressions. Polynomials are algebraic expressions consisting of variables (like 'x') raised to non-negative integer powers, combined with constants and addition/subtraction operations.
Understanding polynomial manipulation is crucial in numerous fields:
- Calculus: Polynomials form the foundation of differential and integral calculus. Finding derivatives and integrals of polynomial functions is a fundamental skill in this branch of mathematics.
- Physics: Polynomials are extensively used to model various physical phenomena, such as projectile motion, oscillations, and the behavior of circuits.
- Engineering: Engineers utilize polynomials to design structures, analyze systems, and model complex processes.
- Computer Science: Polynomial interpolation and approximation are used in computer graphics, numerical analysis, and algorithm design.
- Economics: Polynomial functions are used in economic modeling to represent relationships between variables like supply and demand.
Visualizing the Expression: Graphs and Geometric Interpretations
While the algebraic manipulation of x³ x² x³ is straightforward, visualizing the function y = x⁸ can provide valuable insights. The graph of this function is a steep curve passing through the origin (0,0). The function's behavior illustrates the rapid growth of the function as x increases (both positively and negatively for even powers).
Understanding the visual representation of polynomial functions is essential for:
- Data Analysis: Curve fitting using polynomials allows us to model trends and make predictions based on data sets.
- Problem Solving: Visualizing the graph can reveal critical points, such as intercepts, maxima, and minima, helping in problem-solving.
- Communication: Graphs provide an intuitive way to communicate mathematical relationships to a broader audience.
Real-World Applications of Exponential Growth
The concept of exponential growth, inherent in our original expression (and its simplified form, x⁸), is pervasive in the real world. Consider these examples:
- Compound Interest: The growth of money in a savings account with compound interest follows an exponential pattern. The more frequently the interest is compounded, the faster the exponential growth.
- Population Growth: Under ideal conditions, the population of a species can exhibit exponential growth. This is often modeled using exponential functions.
- Spread of Diseases: In the early stages of an epidemic, the number of infected individuals can increase exponentially. Understanding exponential growth is vital in epidemiology for disease control.
- Radioactive Decay: While not directly related to our example of exponential growth, the decay of radioactive materials follows an exponential decay pattern. This is modeled using exponential functions with negative exponents.
Beyond the Basics: Complex Numbers and Beyond
While our discussion has focused primarily on real numbers, the concept of exponents extends seamlessly to the realm of complex numbers. Complex numbers incorporate an imaginary unit, 'i', where i² = -1. This opens up a whole new dimension of mathematical exploration, with applications in fields like signal processing, quantum mechanics, and electrical engineering.
Conclusion: The Enduring Relevance of x³ x² x³
While seemingly simple at first glance, the expression x³ x² x³ offers a gateway to a deeper understanding of fundamental mathematical concepts. Its simplification highlights the power of exponent rules, its relationship to polynomials reveals its importance in various fields, and its connection to exponential growth showcases its relevance in real-world phenomena. This exploration not only strengthens our mathematical abilities but also provides a valuable appreciation for the interconnectedness of different mathematical branches and their profound influence on diverse areas of study and human endeavor. From the simplicity of algebraic manipulation to the complexities of modeling real-world phenomena, the expression x³ x² x³ serves as a potent reminder of the inherent beauty and practical utility of mathematics. Its seemingly simple nature masks a depth of understanding that extends far beyond its initial appearance, underscoring the ever-present potential for discovery and exploration within the fascinating world of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 3 X 2 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.