X 2 X 6 X 3
News Leon
May 03, 2025 · 5 min read
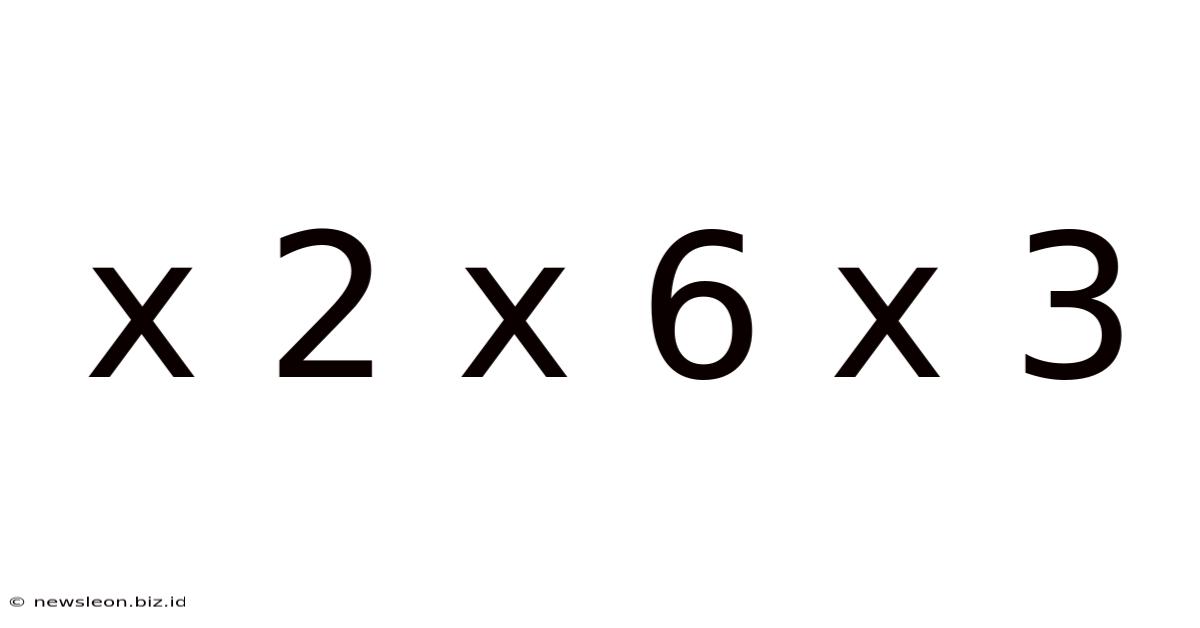
Table of Contents
Decoding the Enigma: Exploring the Mathematical and Conceptual Dimensions of "x 2 x 6 x 3"
The seemingly simple expression "x 2 x 6 x 3" presents a fascinating challenge, opening doors to various mathematical interpretations and conceptual explorations. While its straightforward arithmetic solution is easily calculated, delving deeper reveals a rich landscape of possibilities, touching upon algebra, number theory, and even abstract reasoning. This article aims to unpack this deceptively simple expression, examining its different facets and uncovering the wealth of knowledge hidden within.
The Arithmetic Simplicity: A Straightforward Calculation
At its most basic level, "x 2 x 6 x 3" represents a multiplication problem. If 'x' is treated as a variable or an unknown number, the expression can be simplified through straightforward arithmetic. The order of operations (multiplication is commutative and associative) allows us to perform the multiplications in any order. A common approach is to multiply the constants first: 2 x 6 x 3 = 36. Therefore, the expression simplifies to 36x. This highlights the fundamental role of the variable 'x' – its value determines the final result. This seemingly simple calculation forms the bedrock of our exploration.
Exploring the Significance of 'x'
The variable 'x' in the expression acts as a placeholder, representing an unknown quantity. Its significance lies in its potential to represent a wide range of numerical values, each yielding a unique result when substituted into the equation. This is a core concept in algebra, emphasizing the power of symbolic representation in mathematics. Consider these scenarios:
- If x = 1: The expression evaluates to 36 x 1 = 36
- If x = 0: The expression evaluates to 36 x 0 = 0
- If x = -2: The expression evaluates to 36 x (-2) = -72
- If x = π (pi): The expression evaluates to approximately 36π (approximately 113.097)
This demonstrates how a single algebraic expression can generate a multitude of numerical outcomes, depending solely on the value assigned to the variable. This variability is crucial in solving equations and understanding mathematical relationships.
Beyond Arithmetic: Delving into Algebra and Equations
The expression "x 2 x 6 x 3" transcends its immediate arithmetic interpretation and can be incorporated into algebraic equations. For instance, consider the equation:
36x = 72
Here, our expression (36x) is equated to a known value (72). Solving this equation requires isolating the variable 'x'. By dividing both sides of the equation by 36, we arrive at the solution:
x = 2
This highlights the powerful interplay between arithmetic calculation and algebraic manipulation. We utilized the initial arithmetic simplification of the expression to solve an algebraic equation. Such equations are fundamental to solving numerous problems in various fields, from physics and engineering to finance and economics.
Exploring More Complex Equations
The core expression can be integrated into far more complex equations. Consider this example:
36x + 10 = 100
Here, our simplified expression (36x) forms part of a larger equation. Solving this involves a sequence of steps, including subtraction and division:
- Subtract 10 from both sides: 36x = 90
- Divide both sides by 36: x = 90/36 = 5/2 = 2.5
This example demonstrates how the initial expression can serve as a building block within more complex mathematical structures. The ability to simplify and manipulate such expressions is a cornerstone of algebraic fluency.
The Number Theory Perspective: Exploring Factors and Multiples
From a number theory perspective, the constants within the expression (2, 6, and 3) possess interesting properties. Their product, 36, is a highly composite number, meaning it has a large number of divisors. This richness in factors has significant implications within number theory.
Prime Factorization and its Significance
The prime factorization of 36 is 2² x 3². This representation unveils the fundamental building blocks of the number 36, highlighting its prime factors (2 and 3). Prime factorization is a powerful tool in number theory, used for various applications including cryptography and the study of modular arithmetic. Understanding the prime factorization of the constants in the expression adds another layer to our understanding of its mathematical properties.
Divisibility Rules and Relationships
The numbers 2, 6, and 3 each exhibit specific divisibility rules. The number 36, being their product, inherits and reflects these rules. These divisibility rules provide quick methods for determining whether a number is divisible by 2, 3, or 6, without performing the actual division. This knowledge is useful in various number-theoretic operations and problem-solving scenarios.
Conceptual Extensions and Abstract Interpretations
The expression "x 2 x 6 x 3" can also inspire abstract thinking and conceptual explorations beyond pure arithmetic. It can serve as a starting point for exploring broader mathematical concepts and their applications.
Representing Real-World Scenarios
The expression can be used to model real-world scenarios. For instance, imagine 'x' represents the number of items bought at $36 each. The total cost would be represented by 36x. This demonstrates the expression's practical application in representing simple mathematical relationships in everyday life.
Extending to Higher Dimensions and Operations
The multiplicative nature of the expression can be extended to higher dimensions or more complex operations. For example, the expression could be used as a basis for developing more complex equations or forming part of larger mathematical models.
The Expression as a Building Block
The simple expression "x 2 x 6 x 3" serves as a foundational building block for understanding more advanced mathematical concepts. Its seemingly simple form belies its potential for complexity and its capacity to introduce fundamental principles of algebra, number theory, and mathematical modelling. Mastering the manipulation and interpretation of such expressions is crucial for developing a strong foundation in mathematics.
Conclusion: The Enduring Value of Simplicity
The seemingly simple expression "x 2 x 6 x 3" reveals a depth and complexity that extends far beyond its initial arithmetic calculation. Through its exploration, we have touched upon core concepts of algebra, number theory, and even abstract mathematical reasoning. The expression's power lies in its ability to serve as a springboard for investigating more complex mathematical ideas, highlighting the enduring value of understanding even the most fundamental mathematical constructs. This exploration underscores the importance of approaching mathematical problems with curiosity and a willingness to delve beyond superficial understanding. The seemingly simple can often hold the key to unlocking profound mathematical insights.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 X 6 X 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.