X 2 2xy Y 2 Factored
News Leon
May 05, 2025 · 4 min read
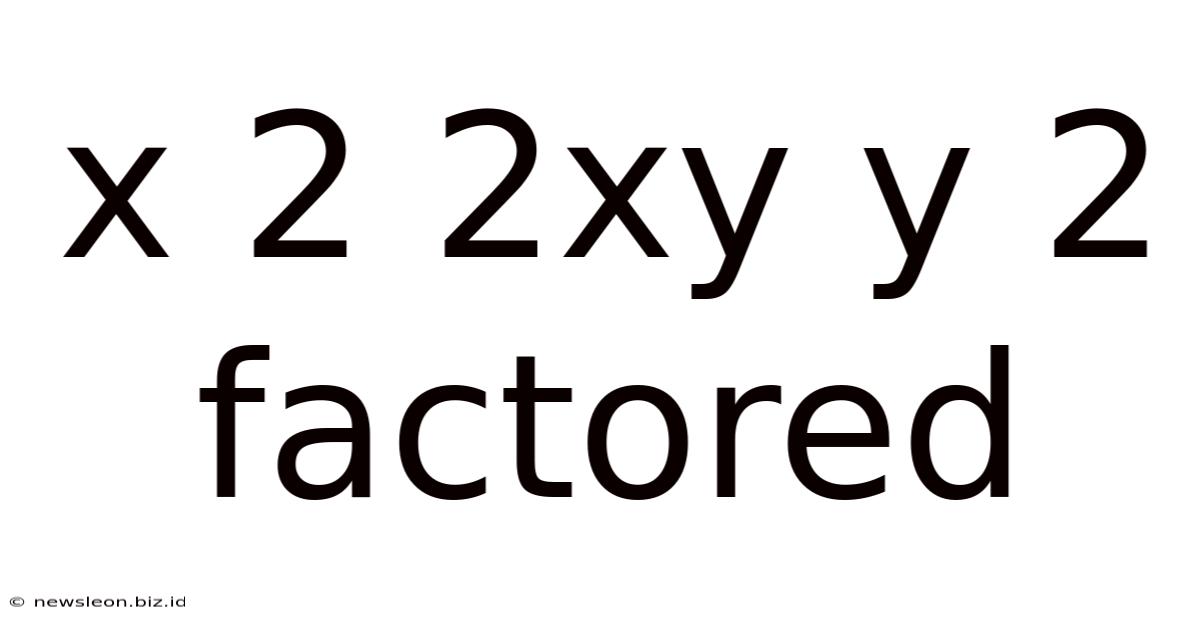
Table of Contents
Factoring x² + 2xy + y²: A Comprehensive Guide
Factoring quadratic expressions is a fundamental skill in algebra. Understanding how to factor these expressions efficiently opens doors to solving complex equations and simplifying algebraic expressions. This comprehensive guide delves into the factorization of the specific trinomial x² + 2xy + y², exploring its underlying principles, various methods of factoring, and practical applications. We'll also explore related concepts and potential pitfalls to avoid.
Understanding the Trinomial x² + 2xy + y²
The trinomial x² + 2xy + y² is a perfect square trinomial. This means it can be factored into the square of a binomial. Recognizing this pattern is crucial for efficient factorization. The key characteristics of a perfect square trinomial are:
- Two terms are perfect squares: In our case,
x²is the square ofx, andy²is the square ofy. - The middle term is twice the product of the square roots of the other two terms: The middle term,
2xy, is twice the product ofxandy(2 * x * y).
Understanding these characteristics allows for quick identification and factorization.
Method 1: Recognizing the Perfect Square Trinomial Pattern
The most efficient way to factor x² + 2xy + y² is by recognizing the perfect square trinomial pattern. This pattern can be generalized as:
a² + 2ab + b² = (a + b)²
In our case, a = x and b = y. Therefore, the factorization is:
x² + 2xy + y² = (x + y)²
This method is direct, quick, and avoids lengthy calculations. It relies on recognizing the specific pattern, which comes with practice.
Method 2: Using the FOIL Method in Reverse
The FOIL method (First, Outer, Inner, Last) is commonly used to expand binomials. We can reverse this process to factor our trinomial. We are looking for two binomials that, when multiplied using FOIL, yield x² + 2xy + y².
Let's assume the factors are of the form (x + ay)(x + by). Expanding this using FOIL gives:
x² + bxy + axy + aby² = x² + (a + b)xy + aby²
Comparing this to our original trinomial, we can see:
- a + b = 2
- ab = 1
By inspection (or solving a simple system of equations), we find that a = 1 and b = 1. Therefore, the factored form is:
(x + 1y)(x + 1y) = (x + y)(x + y) = (x + y)²
This method is more systematic but can be lengthier than recognizing the perfect square trinomial pattern directly.
Method 3: Completing the Square
While less efficient for this specific trinomial, completing the square is a valuable general technique for factoring quadratic expressions. The process involves manipulating the expression to create a perfect square trinomial.
-
Group the x terms: We can rewrite the expression as x² + 2xy + y².
-
Complete the square: Notice that the expression is already a perfect square trinomial; no manipulation is needed. This highlights the efficiency of recognizing the pattern.
-
Factor the perfect square: This step is already done as the expression is in a perfect square trinomial form.
Therefore, completing the square leads to the same result: (x + y)².
Applications of Factoring x² + 2xy + y²
The ability to factor x² + 2xy + y² is essential in various algebraic manipulations and problem-solving scenarios:
-
Simplifying algebraic expressions: Factoring allows for simplifying complex expressions, making them easier to understand and manipulate. For example, (x + y)² is significantly simpler than x² + 2xy + y².
-
Solving quadratic equations: If the equation is in the form x² + 2xy + y² = 0, factoring it to (x + y)² = 0 readily gives the solution x = -y.
-
Calculus: In calculus, factoring is crucial for simplifying derivatives and integrals.
-
Geometry: This factorization finds applications in geometric problems involving areas or volumes described by quadratic expressions.
Potential Pitfalls and Common Mistakes
-
Misidentification of perfect square trinomials: Carefully check if the terms are indeed perfect squares and if the middle term satisfies the condition of being twice the product of the square roots of the outer terms.
-
Incorrect signs: Pay close attention to the signs in the binomial. For example, x² - 2xy + y² factors to (x - y)², not (x + y)².
-
Overlooking simpler methods: For perfect square trinomials, directly recognizing the pattern is the most efficient approach. Avoid unnecessarily complicated methods like completing the square unless necessary.
Expanding the Concept: Variations and Extensions
While we focused on x² + 2xy + y², the principles extend to similar expressions with different coefficients or variables. For instance:
-
4x² + 12xy + 9y²: This is also a perfect square trinomial and factors to (2x + 3y)². Notice how the coefficients are factored into the binomial.
-
(a+b)² + 2(a+b)c + c²: This can be factored as ((a+b) + c)² by letting (a+b) represent a single term. This illustrates the versatility of the perfect square trinomial pattern.
Conclusion
Factoring x² + 2xy + y² to (x + y)² is a straightforward but fundamental algebraic process with wide-ranging applications. By understanding the characteristics of perfect square trinomials and employing efficient methods like pattern recognition, you can master this skill and greatly enhance your ability to solve algebraic problems. Remember to practice regularly and watch out for common pitfalls to solidify your understanding and improve your speed and accuracy. The mastery of this technique is a cornerstone of algebraic fluency, paving the way for tackling more complex mathematical concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about X 2 2xy Y 2 Factored . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.