Write An Equation For The Function Graphed Above
News Leon
Apr 06, 2025 · 6 min read
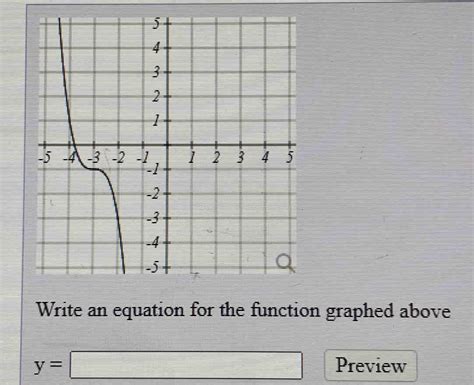
Table of Contents
Decoding the Graph: How to Write an Equation from a Visual Representation
Writing an equation for a function given its graph is a fundamental skill in mathematics. It bridges the gap between the visual and the algebraic, allowing us to express a visual pattern in a precise, symbolic language. This process involves careful observation, pattern recognition, and the application of various mathematical concepts. This comprehensive guide will walk you through different scenarios and techniques to master this skill. We'll explore various function types – linear, quadratic, polynomial, exponential, logarithmic, and trigonometric – and demonstrate how to derive their equations from graphical representations.
Step 1: Identifying the Type of Function
The first, and arguably most crucial, step is correctly identifying the type of function depicted in the graph. This dramatically narrows down the possibilities and dictates the approach you'll take. Look for key visual characteristics:
Linear Functions:
- Straight Line: The defining feature is a straight line.
- Constant Slope: The slope (steepness) remains consistent throughout the line.
- Equation Form: y = mx + c, where 'm' is the slope and 'c' is the y-intercept (where the line crosses the y-axis).
Example: A graph showing a straight line passing through (0, 2) and (1, 5) indicates a linear function. The slope (m) is (5-2)/(1-0) = 3, and the y-intercept (c) is 2. Therefore, the equation is y = 3x + 2.
Quadratic Functions:
- Parabola: The graph forms a U-shaped curve called a parabola.
- Vertex: The parabola has a vertex (highest or lowest point).
- Equation Form: y = ax² + bx + c, where 'a', 'b', and 'c' are constants. The value of 'a' determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
Example: A parabola opening upwards with a vertex at (1, -2) and passing through (0, -1) suggests a quadratic function. Using vertex form, y = a(x - h)² + k, where (h, k) is the vertex, we get y = a(x - 1)² - 2. Substituting (0, -1), we solve for 'a': -1 = a(-1)² - 2, giving a = 1. Thus, the equation is y = (x - 1)² - 2, which can be expanded to y = x² - 2x - 1.
Polynomial Functions:
- Multiple Turns: Polynomial functions of degree 'n' have at most (n-1) turns.
- Smooth Curves: The curves are smooth and continuous, without sharp corners or breaks.
- Equation Form: y = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀, where 'n' is the degree of the polynomial.
Example: A graph with two turns suggests a cubic function (n=3). Determining the equation requires knowing at least three points on the graph or other information like roots (x-intercepts).
Exponential Functions:
- Rapid Growth or Decay: The graph shows increasingly rapid growth or decay.
- Asymptote: Often approaches a horizontal asymptote (a line the graph gets closer to but doesn't cross).
- Equation Form: y = abˣ, where 'a' is the initial value and 'b' is the base (b > 0, b ≠ 1).
Example: A graph showing exponential growth with a y-intercept of 1 and passing through (1, 3) suggests an exponential function. Using the general form, y = abˣ, we have 1 = ab⁰ (which gives a = 1) and 3 = 1*b¹ (which gives b = 3). Therefore, the equation is y = 3ˣ.
Logarithmic Functions:
- Slow Growth: The graph shows slow growth and increases without bound.
- Vertical Asymptote: Often has a vertical asymptote.
- Equation Form: y = a log<sub>b</sub>(x) + c, where 'a', 'b', and 'c' are constants.
Example: A graph showing a logarithmic function with a vertical asymptote at x=0 and passing through (1,0) and (10,1) suggests a base 10 logarithm. We can use the point (10,1) in the equation y = a log₁₀(x). Substituting gives 1 = a log₁₀(10), which means a = 1. Hence, the equation is y = log₁₀(x).
Trigonometric Functions:
- Periodic Nature: The graph repeats its pattern over a regular interval (period).
- Characteristic Shapes: Exhibits shapes like sine waves (smooth oscillations) or cosine waves.
- Equation Form: For sine: y = A sin(Bx + C) + D, where A is the amplitude, B determines the period, C is the phase shift, and D is the vertical shift. Cosine functions have a similar form.
Example: A graph resembling a sine wave with an amplitude of 2 and a period of π suggests a sine function. The general form is y = A sin(Bx). The amplitude (A) is 2. The period is 2π/B = π, so B = 2. Therefore, the equation could be y = 2sin(2x). Note that phase shifts and vertical shifts would alter the specific positioning of the graph.
Step 2: Using Key Points and Information
Once you've identified the function type, you need to extract key information from the graph. This usually involves:
- Intercepts: Where the graph crosses the x-axis (x-intercepts or roots) and the y-axis (y-intercept).
- Vertex (for parabolas): The highest or lowest point.
- Asymptotes: Lines the graph approaches but does not cross.
- Period (for trigonometric functions): The length of one complete cycle.
- Amplitude (for trigonometric functions): The distance from the center line to the peak or trough.
These key points act as data points that can be plugged into the general equation for the identified function type to solve for the unknown constants.
Step 3: Solving for Constants
This step involves using the collected information (key points) to solve for the unknown constants in the general equation. This often involves simultaneous equations or algebraic manipulation.
Example (Quadratic): If a parabola passes through points (0, 1), (1, 0), and (2, 3), we can substitute these coordinates into the general form y = ax² + bx + c:
- For (0, 1): 1 = a(0)² + b(0) + c => c = 1
- For (1, 0): 0 = a(1)² + b(1) + 1
- For (2, 3): 3 = a(2)² + b(2) + 1
Solving these simultaneous equations will provide the values of 'a' and 'b', completing the quadratic equation.
Step 4: Verify Your Equation
After obtaining the equation, it's crucial to verify its accuracy. Check if the equation correctly represents the behavior and key features of the graphed function. You can do this by:
- Plotting points: Plug in different x-values into the equation and check if the resulting y-values correspond to the points on the graph.
- Checking key features: Ensure the equation correctly reflects the intercepts, vertex, asymptotes, period, and amplitude (where applicable).
Advanced Techniques
For more complex graphs or functions, advanced techniques might be required:
- Curve Fitting: Using software or statistical methods to find the best-fitting equation for a set of data points. This is particularly useful for functions that aren't easily identifiable by visual inspection.
- Calculus: Derivatives and integrals can be used to analyze the rate of change and area under the curve, providing additional information to help determine the equation.
Conclusion
Writing an equation from a graph is a multifaceted process that combines visual interpretation with algebraic problem-solving. By carefully identifying the function type, using key points from the graph, and solving for unknown constants, you can effectively translate a visual representation into a precise algebraic equation. Remember to always verify your equation to ensure its accuracy and reflect the essential characteristics of the graphed function. Mastering this skill is paramount to a deeper understanding of functional relationships and their representation in mathematics. Through diligent practice and the application of these techniques, you can confidently tackle a wide range of graphical analysis challenges.
Latest Posts
Latest Posts
-
Atomic Mass Of Al2 So4 3
Apr 09, 2025
-
Area Of Sociology Devoted To The Study Of Human Populations
Apr 09, 2025
-
The Valence Of An Element Or Radical Is
Apr 09, 2025
-
0 23 As A Fraction In Simplest Form
Apr 09, 2025
-
Find The Area Of The Number 7
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Write An Equation For The Function Graphed Above . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.