Which Ratio Is Equivalent To 2 5
News Leon
Apr 05, 2025 · 5 min read
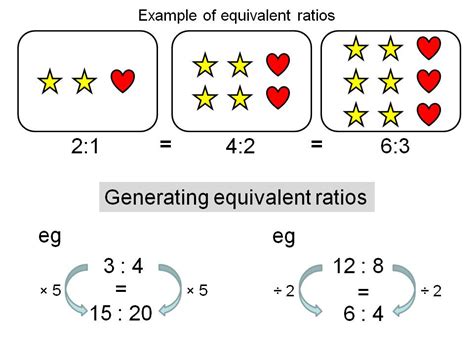
Table of Contents
Which Ratio is Equivalent to 2:5? Understanding Ratio Equivalence and its Applications
Ratios are fundamental mathematical concepts that represent the relative size of two or more values. Understanding ratios and how to find equivalent ratios is crucial in various fields, from cooking and construction to finance and scientific research. This comprehensive guide delves into the concept of ratio equivalence, exploring how to identify ratios equivalent to 2:5, and highlighting its real-world applications.
Understanding Ratios
A ratio is a comparison of two or more quantities. It shows the relationship between these quantities. The ratio 2:5, for instance, means that for every 2 units of one quantity, there are 5 units of another. Ratios can be expressed in several ways:
- Using a colon: 2:5
- As a fraction: 2/5
- Using the word "to": 2 to 5
All three representations convey the same information: the relative proportion of two quantities.
Finding Equivalent Ratios
Equivalent ratios represent the same proportional relationship. They are essentially scaled versions of the original ratio. To find an equivalent ratio, you multiply or divide both parts of the ratio by the same non-zero number. This maintains the proportional relationship.
Let's illustrate this with the ratio 2:5. We can find equivalent ratios by multiplying both the numerator and the denominator by the same number:
- Multiply by 2: (2 x 2) : (5 x 2) = 4:10
- Multiply by 3: (2 x 3) : (5 x 3) = 6:15
- Multiply by 4: (2 x 4) : (5 x 4) = 8:20
- Multiply by 5: (2 x 5) : (5 x 5) = 10:25
- And so on...
Similarly, we can find equivalent ratios by dividing both parts of the ratio by the same number (provided it divides both parts evenly): While 2:5 cannot be simplified by dividing by a whole number (it's already in its simplest form), larger equivalent ratios can be simplified back to 2:5. For example:
- 10:25 divided by 5: (10/5) : (25/5) = 2:5
- 12:30 divided by 6: (12/6) : (30/6) = 2:5
- 20:50 divided by 10: (20/10) : (50/10) = 2:5
Therefore, 4:10, 6:15, 8:20, 10:25, and infinitely many others are equivalent to 2:5.
Simplifying Ratios
A ratio is in its simplest form when the greatest common divisor (GCD) of its parts is 1. This means there's no whole number greater than 1 that can divide both parts of the ratio evenly. The ratio 2:5 is already in its simplest form because the GCD of 2 and 5 is 1.
Real-World Applications of Ratio Equivalence
Understanding ratio equivalence is essential in various practical scenarios:
1. Cooking and Baking:
Recipes often use ratios to specify ingredient proportions. If a recipe calls for a 2:5 ratio of sugar to flour, you can easily scale it up or down by finding equivalent ratios. For example, doubling the recipe would mean using a 4:10 ratio (equivalent to 2:5).
2. Construction and Engineering:
Blueprints and architectural plans frequently employ ratios to represent scale. A 1:100 scale means that 1 unit on the plan represents 100 units in real life. Equivalent ratios are used to convert measurements from the plan to the actual dimensions.
3. Finance and Economics:
Ratios are extensively used in financial analysis to evaluate a company's performance. For example, the debt-to-equity ratio compares a company's debt to its equity. Understanding equivalent ratios can help in comparing companies of different sizes.
4. Science and Chemistry:
In chemistry, ratios are crucial in stoichiometry, which deals with the quantitative relationships between reactants and products in chemical reactions. Equivalent ratios help determine the amounts of reactants needed to produce a specific amount of product.
5. Mapmaking and Geography:
Maps use scale ratios to represent distances on the ground. Understanding equivalent ratios is vital to accurately interpret distances and locations on a map.
6. Everyday Life:
Even simple everyday tasks might involve ratios. For example, mixing paint colors often involves specific ratios to achieve the desired shade. Understanding equivalent ratios helps ensure consistent results.
Identifying Equivalent Ratios: Practical Examples
Let's examine some examples to solidify our understanding:
Example 1: A fruit salad recipe uses a 2:5 ratio of strawberries to blueberries. If you want to make a larger batch using 10 strawberries, how many blueberries do you need?
To find the equivalent ratio, we set up a proportion:
2/5 = 10/x
Cross-multiply: 2x = 50
Solve for x: x = 25
Therefore, you would need 25 blueberries.
Example 2: A map has a scale of 1:50,000. If the distance between two points on the map is 2 centimeters, what is the actual distance between these points?
First, convert centimeters to kilometers for consistency: 2 cm = 0.00002 km
Then, set up the proportion:
1/50,000 = 0.00002/x
Cross-multiply: x = 1 km
Therefore, the actual distance is 1 kilometer.
Example 3: A company's debt-to-equity ratio is 2:5. If the company's debt is $2 million, what is its equity?
Set up the proportion:
2/5 = 2,000,000/x
Cross-multiply: 2x = 10,000,000
Solve for x: x = 5,000,000
The company's equity is $5 million.
Conclusion
The ratio 2:5, and its many equivalent ratios, represents a fundamental concept with widespread applicability. From scaling recipes to analyzing financial statements, understanding how to identify and work with equivalent ratios is a valuable skill across diverse fields. By mastering these concepts, you'll be better equipped to solve problems, interpret data, and make informed decisions in various real-world scenarios. The ability to quickly and accurately determine equivalent ratios is a key element of numeracy and a powerful tool for problem-solving in many aspects of life. Practice is key to mastering this skill; the more you work with ratios, the more intuitive the process will become.
Latest Posts
Latest Posts
-
Eukaryotic Cells May Contain All Of The Following Except
Apr 06, 2025
-
An Infinitely Long Straight Cylindrical Wire
Apr 06, 2025
-
Definition Of Economic Activity In Geography
Apr 06, 2025
-
Which Of The Following Statements Is True About Electronic Commerce
Apr 06, 2025
-
Which Of The Following Is Part Of The Cell Theory
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Which Ratio Is Equivalent To 2 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
