Which Quadrilaterals Have Diagonals That Bisect Each Other
News Leon
Mar 31, 2025 · 5 min read
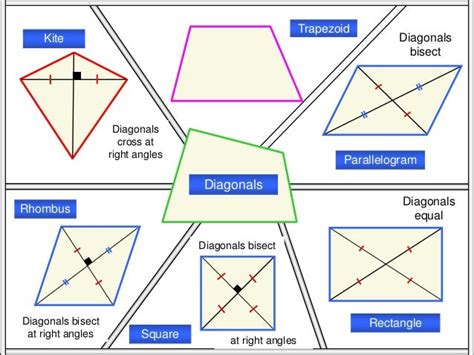
Table of Contents
Which Quadrilaterals Have Diagonals That Bisect Each Other?
Understanding the properties of quadrilaterals is fundamental in geometry. One key characteristic that distinguishes different types of quadrilaterals is whether their diagonals bisect each other. This seemingly simple property has significant implications for classifying and analyzing these four-sided shapes. This in-depth article will explore which quadrilaterals possess this specific characteristic, delving into the proofs and implications of this geometric feature.
Defining the Terms
Before we dive into the specifics, let's clarify some essential terminology:
-
Quadrilateral: A polygon with four sides and four angles. Examples include squares, rectangles, parallelograms, rhombuses, trapezoids, and kites.
-
Diagonal: A line segment connecting two non-adjacent vertices of a polygon. In a quadrilateral, there are two diagonals.
-
Bisect: To divide something into two equal parts. In the context of diagonals, it means that the intersection point divides each diagonal into two segments of equal length.
Quadrilaterals with Diagonals That Bisect Each Other
The crucial point to remember is that not all quadrilaterals have diagonals that bisect each other. This property is exclusive to certain types:
-
Parallelograms: A parallelogram is a quadrilateral where opposite sides are parallel and equal in length. This is the most fundamental quadrilateral whose diagonals bisect each other. This property forms the basis for many proofs and theorems involving parallelograms.
- Proof: Consider parallelogram ABCD, where AB is parallel to CD and BC is parallel to AD. Draw diagonals AC and BD intersecting at point O. Using alternate interior angles and properties of parallel lines, we can prove that triangles ABO and CDO are congruent. Similarly, triangles BCO and ADO are congruent. This congruence proves that AO = OC and BO = OD, meaning the diagonals bisect each other.
-
Rectangles: A rectangle is a special case of a parallelogram where all angles are right angles (90 degrees). Since a rectangle is a parallelogram, it inherits the property that its diagonals bisect each other. Additionally, in a rectangle, the diagonals are equal in length.
-
Rhombuses: A rhombus is a parallelogram where all sides are equal in length. Like rectangles, rhombuses are parallelograms, and thus their diagonals bisect each other. However, unlike rectangles, the diagonals of a rhombus are not necessarily equal in length; they are perpendicular bisectors of each other.
-
Squares: A square is a special case of both a rectangle and a rhombus. Therefore, a square inherits the property of having diagonals that bisect each other. In a square, the diagonals are equal in length and perpendicular bisectors of each other.
Quadrilaterals Whose Diagonals Do NOT Bisect Each Other
It's equally important to understand which quadrilaterals do not have diagonals that bisect each other. These include:
-
Trapezoids (Trapeziums): A trapezoid is a quadrilateral with at least one pair of parallel sides. In general, the diagonals of a trapezoid do not bisect each other. There's an exception – an isosceles trapezoid, where the non-parallel sides are equal in length, possesses diagonals of equal length, but they still do not bisect each other.
-
Kites: A kite is a quadrilateral with two pairs of adjacent sides that are equal in length. The diagonals of a kite are perpendicular, but only one diagonal is bisected by the other. The diagonal connecting the vertices of the unequal sides is bisected, while the other diagonal is not.
Implications and Applications
The property of diagonals bisecting each other has significant implications in various areas:
-
Coordinate Geometry: This property simplifies calculations involving the coordinates of vertices. Finding the midpoint of the diagonals can be used to determine other properties of the quadrilateral.
-
Vector Geometry: Vector representations of the diagonals and their bisected points can be used for solving problems involving forces and displacements.
-
Proofs and Theorems: The fact that the diagonals of a parallelogram bisect each other serves as a foundation for many geometric proofs and theorems concerning parallelograms and related shapes.
-
Construction and Design: Understanding this property helps in constructing various structures and designs involving quadrilateral shapes, ensuring stability and symmetry.
Further Exploration: Isosceles Trapezoids
While the diagonals of a general trapezoid do not bisect each other, the isosceles trapezoid presents a unique case. In an isosceles trapezoid, the non-parallel sides are equal in length. While the diagonals do not bisect each other, they are equal in length. This seemingly small difference highlights the nuances within the broader category of quadrilaterals.
Distinguishing Between Quadrilaterals Based on Diagonal Properties
The properties of diagonals provide a powerful tool for distinguishing between different types of quadrilaterals. Consider these characteristics:
| Quadrilateral | Diagonals Bisect Each Other? | Diagonals Perpendicular? | Diagonals Equal Length? |
|---|---|---|---|
| Parallelogram | Yes | No | No |
| Rectangle | Yes | No | Yes |
| Rhombus | Yes | Yes | No |
| Square | Yes | Yes | Yes |
| Trapezoid | No | Usually No | Usually No |
| Isosceles Trapezoid | No | Usually No | Yes |
| Kite | No (only one is bisected) | Yes | No |
This table clearly illustrates how the properties of the diagonals can help in identifying specific types of quadrilaterals.
Conclusion
Determining which quadrilaterals have diagonals that bisect each other is a crucial concept in geometry. While this property is inherent in parallelograms and their special cases (rectangles, rhombuses, and squares), it is absent in other quadrilaterals like trapezoids and kites. Understanding this distinction is not only important for classifying quadrilaterals but also for solving various geometric problems, from coordinate geometry to vector applications and proving theorems. This deep dive into the properties of quadrilateral diagonals provides a solid foundation for further exploration in geometry and related fields. By carefully examining the characteristics of each quadrilateral type and understanding the implications of diagonal properties, we gain a more comprehensive and nuanced understanding of this fundamental aspect of geometric shapes. The ability to identify and utilize these geometric properties is a crucial skill for any student or professional working within the fields of mathematics, engineering, architecture, and design.
Latest Posts
Latest Posts
-
Which Of The Following Has A Negative Charge
Apr 01, 2025
-
Is Ribose An Aldose Or Ketose
Apr 01, 2025
-
Cartilaginous Fishes And Bony Fishes Are Different In That Only
Apr 01, 2025
-
Which Statement Is Not True Regarding Muscle Contraction
Apr 01, 2025
-
Secondary Pollutants Are More Harmful Than Primary Pollutants
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Which Quadrilaterals Have Diagonals That Bisect Each Other . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
