Which Kind Of Triangle Is Shown
News Leon
Apr 05, 2025 · 6 min read
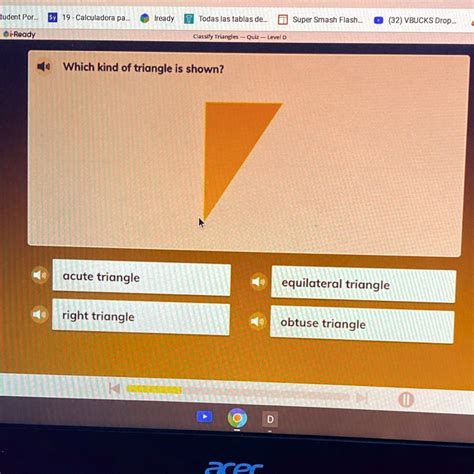
Table of Contents
Which Kind of Triangle is Shown? A Deep Dive into Triangle Classification
Identifying different types of triangles is a fundamental concept in geometry. While seemingly simple, understanding the various classifications – based on side lengths and angles – opens the door to more complex geometric theorems and applications. This comprehensive guide explores the different types of triangles, providing clear definitions, examples, and helpful tips for identification. We'll delve into how to accurately determine which kind of triangle is shown, regardless of its orientation or the information provided.
Understanding Triangle Classification: Sides and Angles
Triangles are classified based on two primary characteristics: their side lengths and their angles. Let's examine each classification system:
Classification by Side Lengths
-
Equilateral Triangle: An equilateral triangle has three sides of equal length. Consequently, all its angles are also equal (60° each). This is the most symmetrical type of triangle. Think of the classic triangular shape often used in logos or decorative patterns.
-
Isosceles Triangle: An isosceles triangle possesses at least two sides of equal length. The angles opposite these equal sides are also equal. Many common geometric figures incorporate isosceles triangles, demonstrating their versatility in design and construction.
-
Scalene Triangle: A scalene triangle has three sides of unequal length. Correspondingly, all its angles are also unequal. This type of triangle exhibits the least symmetry among the three classifications based on side lengths. Think of the irregular triangles you might find in nature, like the shape of a leaf or a section of a jagged coastline.
Classification by Angles
-
Acute Triangle: An acute triangle has three acute angles (angles less than 90°). All the angles are smaller than a right angle. The sum of its internal angles, as with all triangles, always equals 180°.
-
Right Triangle: A right triangle contains one right angle (a 90° angle). The side opposite the right angle is called the hypotenuse, and it's the longest side of the triangle. This is a critical type of triangle in trigonometry and many practical applications.
-
Obtuse Triangle: An obtuse triangle features one obtuse angle (an angle greater than 90°). The other two angles are acute (less than 90°). The presence of one obtuse angle immediately distinguishes it from acute and right triangles.
Combining Classifications: A Powerful Tool
It's important to understand that a triangle can be classified in two ways simultaneously. For example, a triangle can be both an isosceles triangle (based on its sides) and an acute triangle (based on its angles). This dual classification provides a more comprehensive description of the triangle's properties. Similarly, a triangle might be a scalene triangle and an obtuse triangle.
How to Identify the Type of Triangle Shown
Let's move beyond the theoretical definitions and explore practical methods for identifying triangle types:
1. Visual Inspection: The Quick Check
The simplest method is visual inspection. By observing the triangle's shape, you can often make an initial determination. Look for:
-
Equal side lengths: If sides appear equal, it's likely an equilateral or isosceles triangle. Look for markings indicating equal lengths.
-
Right angle: The presence of a square in the corner signifies a 90° angle, identifying a right triangle.
-
Obtuse angle: An angle that clearly exceeds 90° visually indicates an obtuse triangle.
However, relying solely on visual inspection can be unreliable, especially with imprecisely drawn diagrams. Measurements or additional information are essential for accurate classification.
2. Using Measurements: The Accurate Approach
The most reliable way to determine a triangle's type is to measure its sides and angles. Using a ruler and protractor (or digital tools), you can accurately determine:
-
Side lengths: Measure each side length to determine if they're equal or unequal. Slight variations may occur due to measurement inaccuracies, so consider a margin of error.
-
Angles: Measure each angle using a protractor to determine whether they are acute, right, or obtuse. Again, account for possible measurement error.
Based on the measurements obtained, you can confidently classify the triangle according to both its sides and angles.
3. Using Given Information: Working with Data
Sometimes, the problem provides information about side lengths or angles. In these cases, you can directly apply the definitions:
-
Given side lengths: If the problem states the lengths of the three sides, compare them to determine whether the triangle is equilateral, isosceles, or scalene.
-
Given angles: If the angles are given, determine whether they are acute, right, or obtuse. Remember the sum of angles in any triangle must be 180°.
By using the given data, you avoid the need for measurements and can directly apply the definitions to classify the triangle.
Solving Problems: Real-World Examples
Let's work through a few examples to solidify your understanding:
Example 1:
A triangle has sides of length 5 cm, 5 cm, and 7 cm. What type of triangle is it?
Solution:
Since two sides are equal (5 cm and 5 cm), it's an isosceles triangle. The fact that the third side is different means it cannot be equilateral. To determine if it's acute, right, or obtuse, we'd need to calculate the angles.
Example 2:
A triangle has angles measuring 30°, 60°, and 90°. What type of triangle is it?
Solution:
This triangle is a right triangle (due to the 90° angle) and a scalene triangle (since all angles are different).
Example 3:
A triangle has sides of length 8 cm, 8 cm, and 8 cm. What type of triangle is it?
Solution:
All three sides are equal, so it's an equilateral triangle. It is also an acute triangle because all angles are equal and less than 90° (each angle is 60°).
Advanced Concepts and Applications
Understanding triangle classification is crucial for tackling more advanced geometric concepts:
-
Trigonometry: Right triangles are fundamental in trigonometry, used to solve problems involving angles and side lengths.
-
Geometric proofs: Triangle classifications are often used in geometrical proofs to establish relationships between different parts of the triangle.
-
Engineering and architecture: Different types of triangles are used in various engineering and architectural designs, exploiting their stability and structural properties.
Conclusion: Mastering Triangle Identification
Identifying the type of triangle shown is a crucial skill in geometry. This guide has provided you with the tools and understanding to accurately classify triangles based on both their side lengths and angles. By combining visual inspection, measurements, and utilizing given information, you can confidently determine whether a triangle is equilateral, isosceles, scalene, acute, right, or obtuse – or a combination of these classifications. Remember, practice is key. The more you work through examples and apply these methods, the more proficient you'll become in identifying the type of triangle presented. This fundamental understanding will serve you well as you progress to more advanced geometrical concepts and real-world applications.
Latest Posts
Latest Posts
-
Balance Equation Naoh H2so4 Na2so4 H2o
Apr 05, 2025
-
Non Metal Liquid At Room Temp
Apr 05, 2025
-
Which Of The Following Is An Example Of Pollution
Apr 05, 2025
-
Which Of The Following Is Not Characteristic Of Metals
Apr 05, 2025
-
Whats The Difference Between Mg And Ml
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Which Kind Of Triangle Is Shown . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
