Which Is A Factor Of X2-9x+14
News Leon
May 05, 2025 · 5 min read
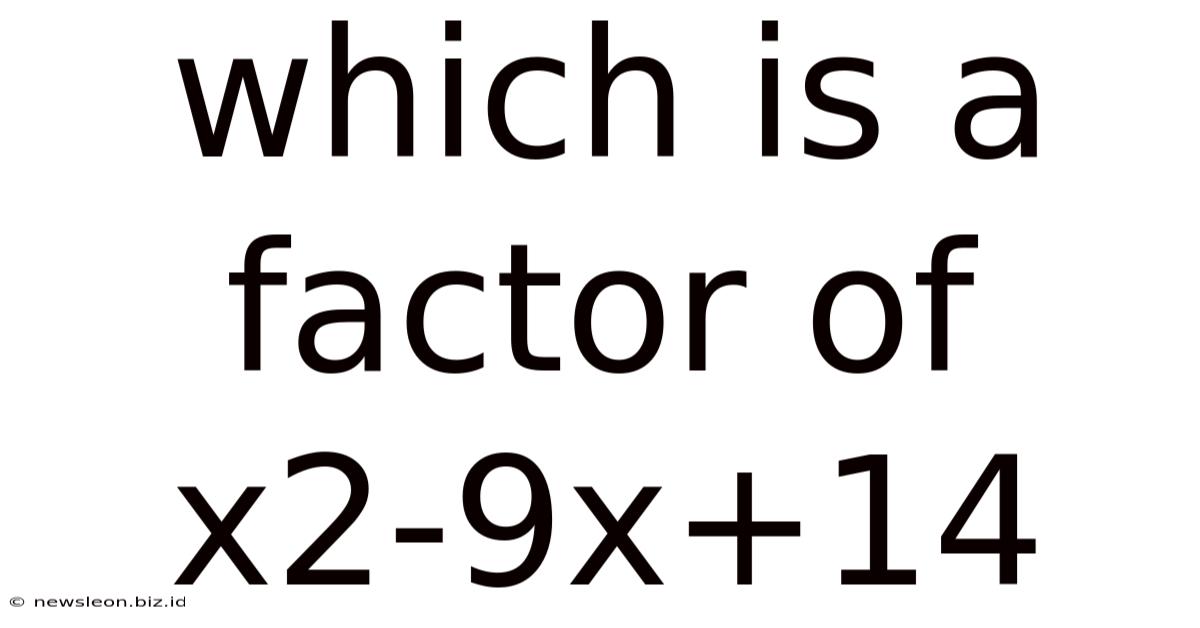
Table of Contents
Which is a Factor of x² - 9x + 14? A Deep Dive into Quadratic Factoring
Finding the factors of a quadratic expression is a fundamental concept in algebra. This article will explore how to determine the factors of the quadratic expression x² - 9x + 14, providing a detailed explanation and examining various approaches to solving such problems. We'll go beyond simply finding the answer; we'll delve into the underlying principles and demonstrate how these techniques can be applied to a broader range of quadratic expressions.
Understanding Quadratic Expressions
A quadratic expression is a polynomial of degree two, meaning the highest power of the variable (usually x) is 2. It generally takes the form ax² + bx + c, where a, b, and c are constants. In our case, we have the quadratic expression x² - 9x + 14, where a = 1, b = -9, and c = 14.
Method 1: Factoring by Inspection (Trial and Error)
This method involves finding two numbers that add up to the coefficient of the x term (b) and multiply to the constant term (c). In our expression, x² - 9x + 14:
- The sum of the two numbers must be -9 (b).
- The product of the two numbers must be 14 (c).
Let's consider the factors of 14: 1 and 14, 2 and 7. Since the sum needs to be -9 and the product is positive, both numbers must be negative. Therefore, -2 and -7 satisfy both conditions:
- -2 + (-7) = -9
- -2 * (-7) = 14
This means we can factor the quadratic expression as (x - 2)(x - 7).
Therefore, the factors of x² - 9x + 14 are (x - 2) and (x - 7).
Method 2: Completing the Square
This method is more involved but provides a systematic approach to factoring quadratics, especially those that are not easily factored by inspection. The goal is to manipulate the expression to create a perfect square trinomial.
-
Move the constant term to the right side: x² - 9x = -14
-
Take half of the coefficient of the x term (-9), square it ((-9/2)² = 81/4), and add it to both sides:
x² - 9x + 81/4 = -14 + 81/4
-
Factor the left side as a perfect square:
(x - 9/2)² = -56/4 + 81/4 = 25/4
-
Take the square root of both sides:
x - 9/2 = ±√(25/4) = ±5/2
-
Solve for x:
x = 9/2 ± 5/2
x = 7 or x = 2
-
Express in factored form: Since x = 7 and x = 2 are the roots, the factors are (x - 7) and (x - 2).
Therefore, the factors of x² - 9x + 14 are (x - 2) and (x - 7). While this method is more complex for this specific example, it's invaluable for factoring quadratics that are less straightforward.
Method 3: Using the Quadratic Formula
The quadratic formula is a powerful tool for finding the roots (solutions) of any quadratic equation of the form ax² + bx + c = 0. The formula is:
x = [-b ± √(b² - 4ac)] / 2a
For our expression x² - 9x + 14 = 0, we have a = 1, b = -9, and c = 14. Plugging these values into the quadratic formula:
x = [9 ± √((-9)² - 4 * 1 * 14)] / (2 * 1)
x = [9 ± √(81 - 56)] / 2
x = [9 ± √25] / 2
x = [9 ± 5] / 2
x = 7 or x = 2
Again, the roots are 7 and 2, leading to the factors (x - 7) and (x - 2).
Therefore, the factors of x² - 9x + 14 are (x - 2) and (x - 7).
Expanding on the Concepts: Applications and Further Exploration
Understanding quadratic factoring extends far beyond simply finding the factors of a single expression. It's a cornerstone of numerous algebraic concepts and applications:
1. Solving Quadratic Equations:
Factoring allows us to solve quadratic equations easily. If a quadratic expression is factored into (x - a)(x - b) = 0, then the solutions (roots) are x = a and x = b. This is because the product of two factors is zero only if at least one of the factors is zero.
2. Graphing Parabolas:
The roots of a quadratic equation represent the x-intercepts of the parabola represented by the quadratic function. Knowing the factors helps in accurately sketching the parabola.
3. Calculus:
Quadratic factoring plays a crucial role in finding critical points and analyzing the behavior of functions in calculus.
4. Physics and Engineering:
Quadratic equations frequently appear in physics and engineering applications, such as projectile motion and circuit analysis. The ability to factor these equations is essential for solving practical problems.
Dealing with More Complex Quadratic Expressions
The methods outlined above can be applied to a wider range of quadratic expressions, even those with a leading coefficient (a) other than 1. For example, let's consider 2x² + 7x + 3:
While inspection might be more challenging, we can still use the other methods: completing the square or the quadratic formula. The quadratic formula remains a reliable approach for all quadratic equations, regardless of their complexity.
Conclusion: Mastering Quadratic Factoring
Mastering quadratic factoring is a crucial skill in algebra and beyond. This article has demonstrated three effective methods: factoring by inspection, completing the square, and using the quadratic formula. Understanding these methods equips you to solve quadratic equations, graph parabolas, and tackle more advanced mathematical concepts. Remember to practice regularly to solidify your understanding and develop your ability to efficiently factor various quadratic expressions. The ability to swiftly and accurately factor quadratics will significantly enhance your problem-solving skills in mathematics and related fields. This deep understanding will serve as a strong foundation for tackling more complex mathematical challenges in your future studies.
Latest Posts
Related Post
Thank you for visiting our website which covers about Which Is A Factor Of X2-9x+14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.