What Quadrilaterals Have Diagonals That Bisect Each Other
News Leon
Apr 03, 2025 · 5 min read
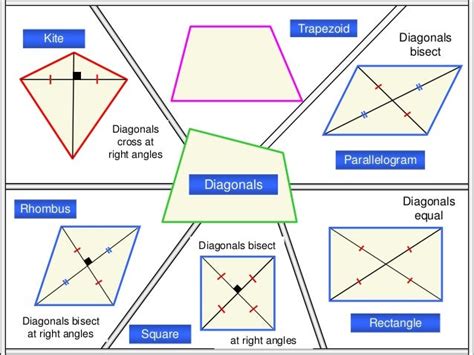
Table of Contents
What Quadrilaterals Have Diagonals That Bisect Each Other?
Understanding the properties of quadrilaterals is crucial in geometry. One key characteristic used to classify quadrilaterals is whether their diagonals bisect each other. This seemingly simple property actually narrows down the possibilities significantly. Let's explore which quadrilaterals possess this characteristic and delve into the reasons why.
Defining the Terms
Before we dive into the specifics, let's clarify some essential geometric terms:
- Quadrilateral: A polygon with four sides and four angles. Examples include squares, rectangles, parallelograms, rhombuses, trapezoids, and kites.
- Diagonal: A line segment connecting two non-adjacent vertices of a polygon. In a quadrilateral, there are two diagonals.
- Bisect: To divide something into two equal parts. If a diagonal bisects another, it means it cuts it precisely in half at their point of intersection.
Quadrilaterals with Mutually Bisecting Diagonals
The key characteristic we're examining is whether the diagonals of a quadrilateral bisect each other. This property significantly limits the types of quadrilaterals we're considering. The quadrilaterals whose diagonals bisect each other are:
-
Parallelograms: This is the broadest category of quadrilaterals whose diagonals bisect each other. A parallelogram is defined as a quadrilateral with opposite sides parallel. This inherent parallelism directly leads to the property of bisecting diagonals.
-
Rectangles: A rectangle is a special type of parallelogram where all four angles are right angles (90 degrees). Since a rectangle is a parallelogram, its diagonals automatically bisect each other.
-
Rhombuses: A rhombus is a parallelogram where all four sides are of equal length. Again, because it's a parallelogram, its diagonals bisect each other. Interestingly, the diagonals of a rhombus also bisect the angles of the rhombus.
-
Squares: A square is the most specialized quadrilateral in this group. It's both a rectangle (right angles) and a rhombus (equal sides). Consequently, it inherits the property of mutually bisecting diagonals.
Proof: Why Parallelograms Have Bisecting Diagonals
Let's prove why the diagonals of a parallelogram bisect each other. This proof will highlight the fundamental connection between parallelism and this property.
Theorem: The diagonals of a parallelogram bisect each other.
Proof:
Consider a parallelogram ABCD, where AB is parallel to CD and BC is parallel to AD. Let the diagonals AC and BD intersect at point E. We need to show that AE = EC and BE = ED.
-
Triangles ABE and CDE: Consider triangles ABE and CDE. We know that AB is parallel to CD (definition of parallelogram). Also, angle ABE is equal to angle CDE (alternate interior angles formed by parallel lines and a transversal). Similarly, angle BAE is equal to angle DCE (alternate interior angles). Finally, AB = CD (opposite sides of a parallelogram are equal).
-
Congruent Triangles: By the Angle-Side-Angle (ASA) congruence theorem, triangle ABE is congruent to triangle CDE. Congruent triangles have equal corresponding sides.
-
Bisected Diagonals: Since triangle ABE is congruent to triangle CDE, it follows that AE = EC and BE = ED. Therefore, the diagonals AC and BD bisect each other at point E.
Other Quadrilaterals: Why Not Trapezoids and Kites?
Not all quadrilaterals have diagonals that bisect each other. Let's examine why trapezoids and kites are excluded:
-
Trapezoids: A trapezoid is a quadrilateral with at least one pair of parallel sides. However, unless it's a special type of trapezoid (an isosceles trapezoid), its diagonals will not bisect each other. The lack of parallelism between all sides prevents the creation of congruent triangles necessary for the bisecting property.
-
Kites: A kite is a quadrilateral with two pairs of adjacent sides equal in length. While the diagonals of a kite are perpendicular, they generally do not bisect each other. Only in the special case of a rhombus (which is a kite with all sides equal) do the diagonals bisect each other.
Implications and Applications
The property of mutually bisecting diagonals has several implications and applications in various fields:
-
Geometric constructions: Understanding this property is essential for various geometric constructions and proofs. For instance, it's crucial in constructing the center of a parallelogram or proving properties of specific quadrilaterals.
-
Vector geometry: In vector geometry, this property simplifies calculations involving vectors representing the sides and diagonals of a parallelogram.
-
Engineering and architecture: The properties of parallelograms, including their bisecting diagonals, are frequently used in engineering and architectural designs to create stable and symmetrical structures.
-
Computer graphics: In computer graphics, the properties of quadrilaterals, particularly parallelograms, are used in algorithms for rendering and manipulating 2D and 3D shapes.
Distinguishing Quadrilaterals Based on Diagonals
The properties of the diagonals can be a crucial tool for identifying and distinguishing different types of quadrilaterals:
| Quadrilateral | Diagonals Bisect Each Other | Diagonals Perpendicular | Diagonals Equal in Length |
|---|---|---|---|
| Parallelogram | Yes | No | No |
| Rectangle | Yes | No | Equal |
| Rhombus | Yes | Yes | No |
| Square | Yes | Yes | Equal |
| Trapezoid (general) | No | Usually No | Usually Not Equal |
| Isosceles Trapezoid | No | Usually No | Equal |
| Kite | No | Yes | Usually Not Equal |
Advanced Concepts and Further Exploration
For those interested in a deeper dive into this topic, exploring the following concepts would be beneficial:
-
Coordinate geometry: Applying coordinate geometry to prove the properties of quadrilaterals and their diagonals.
-
Vectors: Using vectors to represent and manipulate geometric objects and prove properties.
-
Affine transformations: Examining how affine transformations affect the properties of quadrilaterals and their diagonals.
Conclusion
The property of having diagonals that bisect each other is a powerful tool for classifying and understanding quadrilaterals. While seemingly a simple characteristic, it directly links to fundamental properties like parallelism and symmetry. By understanding this property and its implications, we gain a deeper appreciation for the rich geometry of quadrilaterals and their diverse properties. The ability to accurately identify and differentiate between these shapes is vital in various mathematical, engineering, and design applications. Through exploring this fundamental geometric characteristic, we unlock a pathway to a more profound comprehension of shape and spatial relationships.
Latest Posts
Latest Posts
-
Which Of The Following Is Not True Of Dna
Apr 04, 2025
-
Any Computer Parts That You Can Actually Touch
Apr 04, 2025
-
Which Of The Following Is Hydrophobic
Apr 04, 2025
-
Do Prokaryotes Have A Membrane Bound Organelles
Apr 04, 2025
-
Why Was A Stain Added To The Cheek Cells
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about What Quadrilaterals Have Diagonals That Bisect Each Other . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
