What Number Is 70 Of 45
News Leon
May 05, 2025 · 4 min read
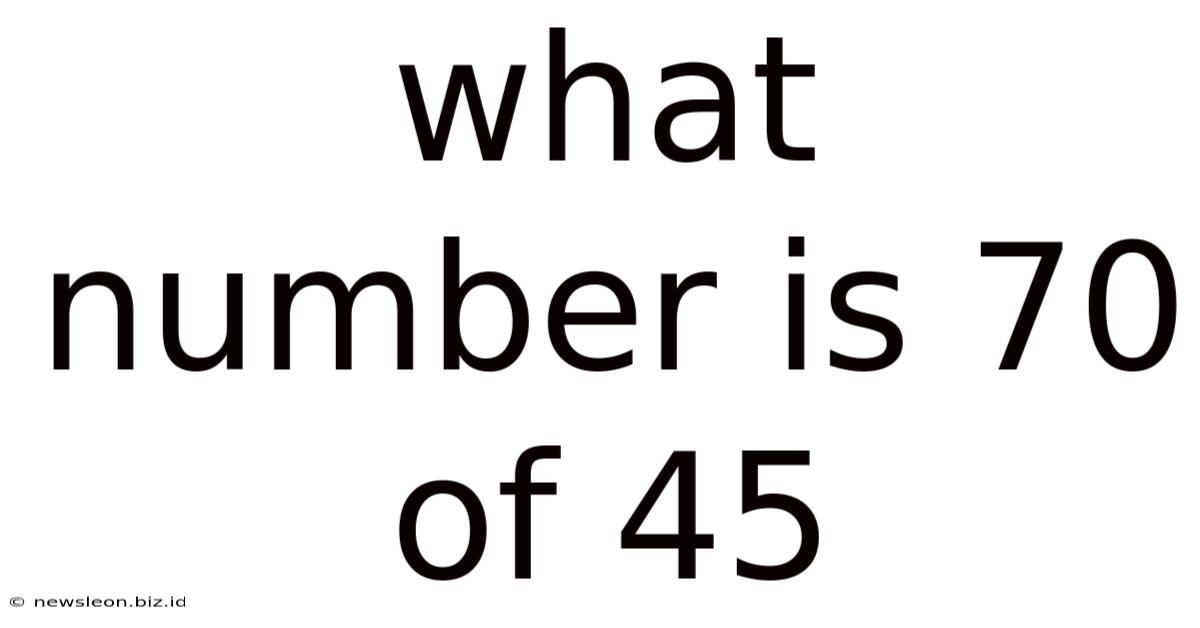
Table of Contents
What Number is 70 of 45? Understanding Percentages and Ratios
The question "What number is 70 of 45?" might seem straightforward at first glance, but it delves into fundamental mathematical concepts like percentages and ratios. Understanding how to solve this, and similar problems, is crucial for everyday life, from calculating discounts to understanding financial reports. This article will not only answer the question directly but also explore the underlying mathematical principles, offering various methods to solve such problems and providing real-world examples.
Deconstructing the Question: Percentages and Ratios
The question, "What number is 70 of 45?", is essentially asking: "What percentage of 45 is 70?" or conversely, "What is the ratio of 70 to 45?". These are two sides of the same coin, reflecting different ways to express the relationship between two numbers. Let's break down each approach.
Understanding Percentages
A percentage is a way of expressing a number as a fraction of 100. It signifies a proportion or rate per hundred. For instance, 50% means 50 out of 100, or 50/100, which simplifies to 1/2.
Understanding Ratios
A ratio compares two or more quantities. In our case, the ratio is 70:45, indicating the relative size of 70 compared to 45. Ratios can be expressed in different ways: using a colon (70:45), as a fraction (70/45), or as a decimal (1.555...).
Solving the Problem: Multiple Approaches
There are several ways to solve "What number is 70 of 45?":
Method 1: Using Proportions
This method uses the concept of equivalent ratios. We set up a proportion:
70/45 = x/100
Where 'x' represents the percentage we want to find. To solve for 'x', we cross-multiply:
45x = 7000
x = 7000 / 45
x ≈ 155.56
Therefore, 70 is approximately 155.56% of 45. This indicates that 70 is significantly larger than 45.
Method 2: Using Decimal Conversion
First, we express the ratio as a fraction: 70/45. Then, we convert this fraction into a decimal by performing the division:
70 ÷ 45 ≈ 1.5556
To express this decimal as a percentage, we multiply by 100:
1.5556 x 100 = 155.56%
This confirms the result obtained using the proportion method.
Method 3: Using a Calculator (Percentage Function)
Most calculators have a percentage function. You can directly input the calculation as: (70/45) * 100 = 155.56%. This is the most straightforward method for quick calculations.
Interpreting the Result: What 155.56% Means
The result, 155.56%, tells us that 70 is 155.56% of 45. This means 70 is larger than 45, exceeding it by 55.56%. It's crucial to understand that percentages greater than 100% represent values exceeding the base value (45 in this case).
Real-World Applications: Practical Examples
Understanding percentages and ratios is essential in numerous real-world scenarios:
Financial Calculations
- Interest rates: Calculating simple or compound interest involves percentages.
- Discounts: Determining the final price after a discount requires understanding percentage reductions.
- Profit margins: Businesses use percentages to calculate profit margins, comparing profit to cost.
- Taxes: Calculating taxes based on income or purchase price necessitates percentage calculations.
- Investment returns: Tracking investment growth often involves percentage changes over time.
Everyday Life
- Cooking: Adjusting recipes based on the number of servings uses ratios and proportions.
- Shopping: Comparing prices and finding the best deals requires calculating unit prices and percentage discounts.
- Travel: Calculating distances and travel times involves ratios and proportions.
- Sports statistics: Many sports statistics are expressed as percentages (e.g., batting averages, free-throw percentages).
Scientific and Engineering Applications
- Scaling models: Creating accurate models requires precise ratios and proportions.
- Data analysis: Percentages and ratios are essential in analyzing data and expressing findings.
- Chemical reactions: Stoichiometry, the study of quantitative relationships in chemical reactions, relies heavily on ratios and proportions.
Beyond the Basics: Further Exploration
While we've addressed the primary question, there are several related concepts worth exploring:
- Percentage change: Calculating the percentage increase or decrease between two values.
- Percentage points: Differentiating between percentage change and percentage points, a common point of confusion.
- Compounding percentages: Understanding how percentages accumulate over time, as seen in compound interest.
- Inverse percentages: Finding the original value after a percentage change has been applied.
Conclusion: Mastering Percentage and Ratio Calculations
The seemingly simple question, "What number is 70 of 45?", unlocks a broader understanding of percentages and ratios—fundamental mathematical concepts with wide-ranging applications. By mastering these concepts, you equip yourself with essential skills for tackling various problems in everyday life, finance, science, and more. Remember the different methods available – using proportions, decimal conversions, or calculators – and choose the method that best suits your needs and comfort level. Understanding these concepts isn't just about solving mathematical problems; it's about developing a practical understanding of how quantities relate to each other, enabling more informed decisions and a clearer grasp of numerical information.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Number Is 70 Of 45 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.