What Is The Sum Of Rational And Irrational Number
News Leon
Apr 08, 2025 · 5 min read
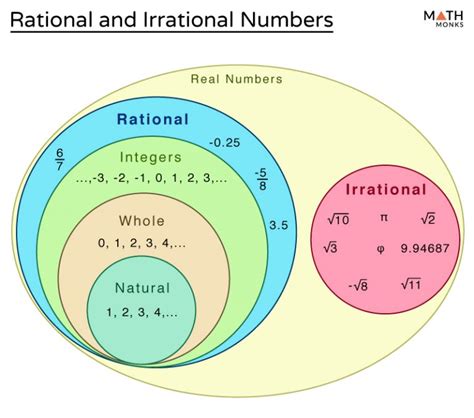
Table of Contents
What is the Sum of a Rational and an Irrational Number?
The question of what happens when you add a rational number and an irrational number is a fundamental concept in mathematics, touching upon the core properties of these number systems. Understanding this requires a grasp of what defines rational and irrational numbers. Let's dive into this fascinating exploration.
Defining Rational and Irrational Numbers
Before we delve into the sum, we need clear definitions:
Rational Numbers:
A rational number is any number that can be expressed as a fraction p/q, where 'p' and 'q' are integers, and 'q' is not zero. This encompasses a wide range of numbers, including:
- Integers: Whole numbers (positive, negative, and zero). Examples: -3, 0, 5, 100.
- Fractions: Numbers expressed as ratios, like 1/2, 3/4, -2/5.
- Terminating Decimals: Decimals that end after a finite number of digits. Examples: 0.25, 0.75, 2.5.
- Repeating Decimals: Decimals with a pattern that repeats infinitely. Examples: 0.333..., 0.666..., 1.234234234...
The key characteristic is the ability to represent the number precisely as a ratio of two integers.
Irrational Numbers:
An irrational number cannot be expressed as a simple fraction of two integers. Their decimal representations are neither terminating nor repeating; they go on forever without any predictable pattern. Famous examples include:
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159... The digits continue infinitely without repeating.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828... Again, an infinite, non-repeating decimal.
- √2 (Square root of 2): This number, approximately 1.414..., cannot be expressed as a fraction of two integers. Its decimal expansion is infinite and non-repeating.
The defining feature is the impossibility of representing them as a ratio of two integers.
Proving the Sum: Rational + Irrational = Irrational
This is where the core of our question lies. Let's prove that the sum of a rational and an irrational number is always irrational. We'll use a proof by contradiction.
1. The Assumption:
Let's assume, for the sake of contradiction, that the sum of a rational number and an irrational number is rational.
2. Defining Variables:
Let 'r' be a rational number (r = p/q, where p and q are integers, q ≠ 0). Let 'i' be an irrational number. We assume that r + i = s, where 's' is a rational number (s = m/n, where m and n are integers, n ≠ 0).
3. Manipulating the Equation:
Since r + i = s, we can rearrange the equation to solve for 'i': i = s - r
4. Substitution and Contradiction:
Substitute the rational expressions for 'r' and 's': i = (m/n) - (p/q)
To subtract these fractions, we find a common denominator (nq): i = (mq - np) / (nq)
Notice that 'mq - np' is an integer (since m, n, p, and q are integers), and 'nq' is also an integer (again, since n and q are integers and q ≠ 0, ensuring the denominator is not zero).
This means we've expressed 'i' as a fraction of two integers – a direct contradiction to our initial definition of 'i' as an irrational number. Irrational numbers, by definition, cannot be expressed as a ratio of two integers.
5. Conclusion:
Our initial assumption – that the sum of a rational and an irrational number is rational – has led to a contradiction. Therefore, the assumption must be false. Consequently, the sum of a rational and an irrational number is always irrational.
Examples Illustrating the Concept
Let's look at some concrete examples to solidify our understanding:
-
Example 1: 5 + √2 ≈ 5 + 1.414 = 6.414... The result is irrational because it's a non-repeating, non-terminating decimal.
-
Example 2: 1/2 + π ≈ 0.5 + 3.14159... = 3.64159... Again, the sum is irrational. Adding a rational fraction to an irrational number doesn't change the irrational nature of the result.
-
Example 3: -3 + e ≈ -3 + 2.71828... = -0.28172... Even when subtracting a rational number from an irrational number (which is essentially adding a negative rational number), the result remains irrational.
-
Example 4: 0.75 + √3 ≈ 0.75 + 1.732 = 2.482... This demonstrates that even with terminating decimals, combined with an irrational number, the result will always be irrational.
In each case, the sum maintains the irrationality of the original irrational number.
Deeper Implications and Applications
The property that the sum of a rational and an irrational number is always irrational has significant implications across various mathematical fields. It underscores the fundamental differences between these number systems and underpins many proofs and theorems in advanced mathematics:
-
Real Number System Completeness: This property contributes to the understanding of the completeness of the real number system. The real numbers encompass both rational and irrational numbers, creating a continuous number line without any gaps.
-
Algebraic Structures: This concept plays a role in the study of algebraic structures and field theory, where properties of number systems are examined abstractly.
-
Limits and Calculus: The distinction between rational and irrational numbers is crucial when dealing with limits and continuity in calculus. Understanding how these types of numbers behave when added together is important for determining convergence and divergence.
-
Number Theory: Number theory heavily relies on the properties of rational and irrational numbers. The inherent properties of these numbers are critical in many theorems and proofs within this area.
Conclusion
The sum of a rational and an irrational number is always irrational. This seemingly simple statement holds profound mathematical implications, highlighting the fundamental difference between these two crucial number sets and impacting our understanding of the real number system and various advanced mathematical concepts. The proof, though concise, demonstrates the power of mathematical reasoning and the elegance of using proof by contradiction to establish important mathematical truths. This understanding forms the foundation for many more complex concepts and problem-solving approaches in various mathematical disciplines.
Latest Posts
Latest Posts
-
5 Protons 6 Neutrons 5 Electrons
Apr 08, 2025
-
The Heart And Blood Vessels Are Lined By
Apr 08, 2025
-
Angular Speed Of Earth Around Sun
Apr 08, 2025
-
Why Did Mendeleev Leave Gaps In The Periodic Table
Apr 08, 2025
-
How Did Renaissance Humanists Differ From Medieval Thinkers
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Sum Of Rational And Irrational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.