What Is The Least Common Multiple Of 24 And 30
News Leon
May 04, 2025 · 5 min read
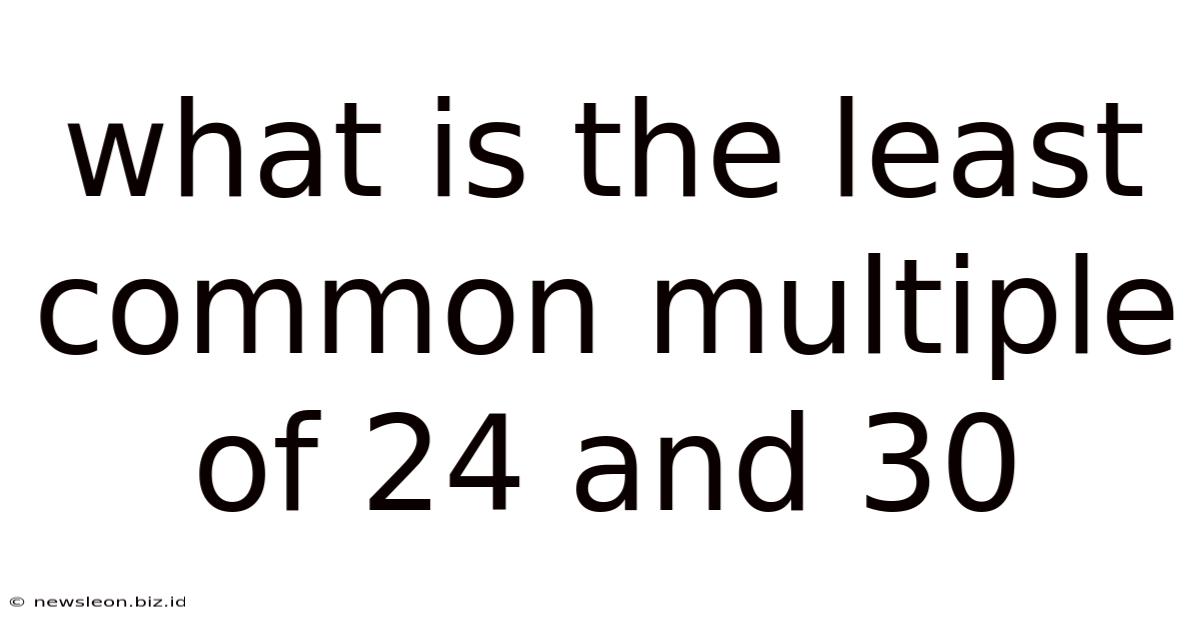
Table of Contents
What is the Least Common Multiple (LCM) of 24 and 30? A Deep Dive into Number Theory
Finding the least common multiple (LCM) of two numbers might seem like a simple mathematical task, but understanding the underlying concepts reveals a fascinating world of number theory with practical applications in various fields. This article delves into the intricacies of determining the LCM of 24 and 30, exploring multiple methods and illustrating the broader significance of this concept in mathematics and beyond.
Understanding Least Common Multiples
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. It's a fundamental concept in number theory with far-reaching implications in areas like scheduling, fractional arithmetic, and even music theory. Unlike the greatest common divisor (GCD), which focuses on the largest number that divides both integers, the LCM focuses on the smallest number that both integers divide.
For instance, consider the numbers 4 and 6. The multiples of 4 are 4, 8, 12, 16, 20, 24, and so on. The multiples of 6 are 6, 12, 18, 24, 30, and so on. The common multiples are 12, 24, 36, etc. The least common multiple is 12.
Methods for Calculating the LCM of 24 and 30
Several methods exist for calculating the LCM of two numbers. Let's explore the most common approaches, applying them to find the LCM of 24 and 30:
1. Listing Multiples Method
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest common multiple.
- Multiples of 24: 24, 48, 72, 96, 120, 144, 168, 192, 216, 240...
- Multiples of 30: 30, 60, 90, 120, 150, 180, 210, 240...
The smallest number appearing in both lists is 120. Therefore, the LCM of 24 and 30 is 120.
This method is simple to understand but becomes cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. We find the prime factorization of each number and then construct the LCM using the highest powers of all prime factors present.
- Prime factorization of 24: 24 = 2³ × 3¹
- Prime factorization of 30: 30 = 2¹ × 3¹ × 5¹
To find the LCM, we take the highest power of each prime factor present in either factorization:
- Highest power of 2: 2³ = 8
- Highest power of 3: 3¹ = 3
- Highest power of 5: 5¹ = 5
Multiplying these together: LCM(24, 30) = 8 × 3 × 5 = 120
This method is generally more efficient than the listing multiples method, particularly for larger numbers.
3. Using the GCD (Greatest Common Divisor)
There's a relationship between the LCM and the GCD of two numbers. The formula is:
LCM(a, b) × GCD(a, b) = a × b
First, let's find the GCD of 24 and 30 using the Euclidean algorithm:
- Divide the larger number (30) by the smaller number (24): 30 = 1 × 24 + 6
- Replace the larger number with the smaller number (24) and the smaller number with the remainder (6): 24 = 4 × 6 + 0
The GCD is the last non-zero remainder, which is 6.
Now, we can use the formula:
LCM(24, 30) = (24 × 30) / GCD(24, 30) = (24 × 30) / 6 = 120
This method is efficient if you already know the GCD. The Euclidean algorithm is a quick way to find the GCD, making this a powerful approach.
Applications of LCM
The concept of the least common multiple has numerous applications across various fields:
1. Scheduling Problems
Imagine two buses arrive at a bus stop at different intervals. Bus A arrives every 24 minutes, and Bus B arrives every 30 minutes. The LCM helps determine when both buses will arrive simultaneously again. The LCM of 24 and 30 is 120 minutes, or 2 hours. Both buses will arrive together again after 2 hours.
2. Fraction Arithmetic
When adding or subtracting fractions with different denominators, the LCM of the denominators is crucial in finding a common denominator. This simplifies the calculation process significantly.
3. Music Theory
LCMs play a role in understanding musical harmony and rhythm. The relationships between musical notes and their frequencies often involve the LCM to identify harmonic intervals.
4. Engineering and Construction
In various engineering and construction projects, the LCM helps synchronize different processes or cycles that have different time periods. This ensures efficient coordination and avoids conflicts.
5. Computer Science
The LCM concept is essential in various algorithms and computations within computer science, particularly those involving modular arithmetic and cyclical processes.
Beyond the Basics: Exploring Further Concepts
Understanding the LCM of 24 and 30 opens doors to more advanced concepts in number theory:
- Modular Arithmetic: The LCM is fundamental in understanding congruences and modular arithmetic, used in cryptography and other areas.
- Diophantine Equations: The LCM often appears in solving Diophantine equations, which are equations involving only integers.
- Abstract Algebra: The concept of LCM generalizes to abstract algebraic structures like rings and ideals, providing a framework for understanding more complex mathematical systems.
Conclusion
Determining the least common multiple of 24 and 30, while seemingly simple, provides a gateway to understanding fundamental principles within number theory. The various methods presented—listing multiples, prime factorization, and using the GCD—illustrate the versatility and power of mathematical tools. Furthermore, the applications of the LCM in diverse fields highlight its practical relevance and demonstrate the interconnectedness of mathematical concepts with the real world. Understanding the LCM is not just about finding a single number; it's about grasping fundamental mathematical relationships that underpin numerous applications and more advanced concepts. Mastering the LCM is a cornerstone to further exploration of the fascinating world of mathematics.
Latest Posts
Related Post
Thank you for visiting our website which covers about What Is The Least Common Multiple Of 24 And 30 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.