What Is The Lcm Of 6 And 20
News Leon
Apr 05, 2025 · 5 min read
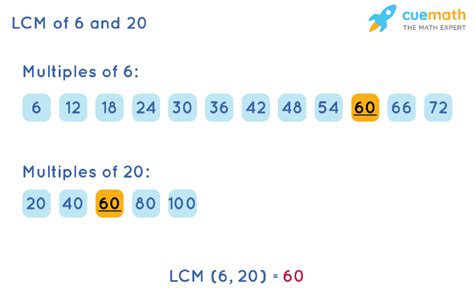
Table of Contents
What is the LCM of 6 and 20? A Deep Dive into Least Common Multiples
Finding the least common multiple (LCM) might seem like a simple arithmetic task, but understanding the underlying concepts and different methods for calculating it opens doors to more complex mathematical applications. This comprehensive guide will not only answer the question "What is the LCM of 6 and 20?" but also explore the broader significance of LCMs in various fields.
Understanding Least Common Multiples (LCM)
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. Think of it as the smallest number that contains all the given numbers as factors. This concept is fundamental in various mathematical operations and real-world applications.
Why is LCM important? The LCM is crucial in various scenarios, including:
- Fraction addition and subtraction: Finding a common denominator for fractions requires determining the LCM of the denominators.
- Scheduling problems: Determining when events will coincide again (e.g., buses arriving at the same stop, machines completing cycles simultaneously) involves finding the LCM of the cycle times.
- Music theory: The LCM is used in determining the least common period of musical rhythms.
- Modular arithmetic: LCM plays a key role in solving congruences and other modular arithmetic problems.
Methods for Calculating the LCM
There are several ways to calculate the LCM of two or more numbers. Let's explore some of the most common methods:
1. Listing Multiples Method
This is a straightforward method, particularly useful for smaller numbers. List the multiples of each number until you find the smallest multiple common to both.
Example: Find the LCM of 6 and 20.
- Multiples of 6: 6, 12, 18, 24, 30, 36, 42, 48, 60, ...
- Multiples of 20: 20, 40, 60, 80, 100, ...
The smallest multiple common to both lists is 60. Therefore, the LCM of 6 and 20 is 60.
This method becomes cumbersome for larger numbers.
2. Prime Factorization Method
This method is more efficient for larger numbers. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor present.
Example: Find the LCM of 6 and 20.
- Prime factorization of 6: 2 × 3
- Prime factorization of 20: 2² × 5
The prime factors are 2, 3, and 5. The highest power of 2 is 2², the highest power of 3 is 3¹, and the highest power of 5 is 5¹.
Therefore, LCM(6, 20) = 2² × 3 × 5 = 4 × 3 × 5 = 60.
This method is generally more efficient than listing multiples, especially for larger numbers or when dealing with multiple numbers.
3. Greatest Common Divisor (GCD) Method
The LCM and GCD (greatest common divisor) of two numbers are related. The product of the LCM and GCD of two numbers is equal to the product of the two numbers.
Formula: LCM(a, b) × GCD(a, b) = a × b
Example: Find the LCM of 6 and 20.
First, find the GCD of 6 and 20 using the Euclidean algorithm or prime factorization.
- Prime factorization of 6: 2 × 3
- Prime factorization of 20: 2² × 5
The common factor is 2. Therefore, GCD(6, 20) = 2.
Now, use the formula:
LCM(6, 20) = (6 × 20) / GCD(6, 20) = 120 / 2 = 60
This method is particularly useful when you already know the GCD of the numbers.
Expanding the Concept: LCM of More Than Two Numbers
The methods described above can be extended to find the LCM of more than two numbers. The prime factorization method is generally the most efficient approach for multiple numbers.
Example: Find the LCM of 6, 15, and 20.
- Prime factorization of 6: 2 × 3
- Prime factorization of 15: 3 × 5
- Prime factorization of 20: 2² × 5
The prime factors are 2, 3, and 5. The highest powers are 2², 3¹, and 5¹.
Therefore, LCM(6, 15, 20) = 2² × 3 × 5 = 4 × 3 × 5 = 60
Real-World Applications of LCM
Beyond the classroom, LCM finds practical applications in various fields:
- Construction: Determining the appropriate lengths of materials for repetitive patterns or structures.
- Manufacturing: Coordinating machine cycles in assembly lines to optimize production.
- Scheduling: Synchronizing events, like coordinating shifts of workers, or planning recurring events.
- Software Development: In algorithm design and task scheduling.
- Cryptography: In some cryptographic algorithms where modular arithmetic is crucial.
Advanced Concepts and Related Topics
Understanding LCM opens doors to more advanced mathematical concepts:
- Modular Arithmetic: LCM is fundamental to solving congruences and other problems in modular arithmetic.
- Abstract Algebra: The concept of LCM generalizes to more abstract algebraic structures like rings and ideals.
- Number Theory: LCM is used in various number theoretic problems and proofs.
Conclusion: Mastering the LCM
The LCM, while seemingly a simple concept, is a powerful tool with far-reaching applications. By understanding the different methods for calculating the LCM and its connections to other mathematical concepts, you equip yourself with a valuable skill for solving a wide array of problems, from simple arithmetic tasks to complex mathematical challenges in various fields. The seemingly simple question, "What is the LCM of 6 and 20?" serves as a gateway to exploring a rich and fascinating area of mathematics. Remember that the LCM of 6 and 20 is 60, and understanding how to arrive at this answer opens up a world of possibilities.
Latest Posts
Latest Posts
-
An Infinitely Long Straight Cylindrical Wire
Apr 06, 2025
-
Definition Of Economic Activity In Geography
Apr 06, 2025
-
Which Of The Following Statements Is True About Electronic Commerce
Apr 06, 2025
-
Which Of The Following Is Part Of The Cell Theory
Apr 06, 2025
-
72 Inches Is Equal To How Many Yards
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is The Lcm Of 6 And 20 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
