What Is The Area Of The Triangle Shown
News Leon
Apr 06, 2025 · 5 min read
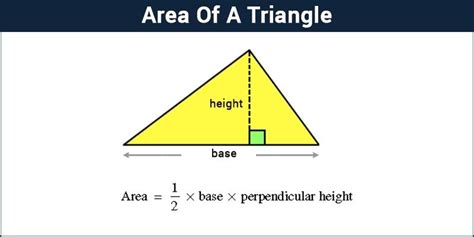
Table of Contents
What is the Area of the Triangle Shown? A Comprehensive Guide
Determining the area of a triangle is a fundamental concept in geometry with applications spanning various fields, from architecture and engineering to computer graphics and data analysis. While the basic formula is relatively straightforward, understanding its nuances and applications requires a deeper dive. This article explores various methods for calculating the area of a triangle, tackling different scenarios and providing practical examples to solidify your understanding.
Understanding the Basic Formula: ½ * base * height
The most common and widely known formula for calculating the area of a triangle is:
Area = ½ * base * height
Where:
- base: The length of any side of the triangle.
- height: The perpendicular distance from the base to the opposite vertex (the highest point of the triangle).
This formula works flawlessly when you know the length of the base and the corresponding height. However, in many real-world scenarios, you might not have this readily available information.
Example 1: A Right-Angled Triangle
Let's consider a right-angled triangle with a base of 6 cm and a height of 8 cm.
Area = ½ * 6 cm * 8 cm = 24 cm²
This is a simple, straightforward application of the formula.
Example 2: An Obtuse Triangle
In an obtuse triangle (a triangle with one angle greater than 90 degrees), the height might fall outside the triangle's base. However, the principle remains the same. Identify the base and its corresponding perpendicular height, and plug the values into the formula.
When Height Isn't Directly Given: Alternative Methods
Often, you'll encounter situations where the height isn't explicitly provided. This necessitates the use of alternative formulas or approaches.
1. Heron's Formula: Using the Lengths of All Three Sides
Heron's formula is exceptionally useful when you know the lengths of all three sides (a, b, c) of the triangle but not the height. It involves calculating the semi-perimeter (s) first:
s = (a + b + c) / 2
Then, the area (A) is calculated as:
A = √[s(s-a)(s-b)(s-c)]
This formula is elegant and powerful because it doesn't require knowledge of the angles or height.
Example 3: Applying Heron's Formula
Consider a triangle with sides of length 5 cm, 6 cm, and 7 cm.
- Calculate the semi-perimeter (s): s = (5 + 6 + 7) / 2 = 9 cm
- Apply Heron's formula: A = √[9(9-5)(9-6)(9-7)] = √[9 * 4 * 3 * 2] = √216 ≈ 14.7 cm²
2. Using Trigonometry: Area = ½ * a * b * sin(C)
Trigonometry provides another powerful tool for calculating the area of a triangle when you know the lengths of two sides (a and b) and the angle (C) between them. The formula is:
Area = ½ * a * b * sin(C)
This formula leverages the sine function to account for the angle's impact on the area.
Example 4: Trigonometric Area Calculation
Let's say we have a triangle with sides a = 10 cm, b = 12 cm, and the angle C between them is 30 degrees.
Area = ½ * 10 cm * 12 cm * sin(30°) = 30 cm² (Remember that sin(30°) = 0.5)
3. Coordinate Geometry: Using the Coordinates of the Vertices
If you know the coordinates of the three vertices of a triangle (x₁, y₁), (x₂, y₂), and (x₃, y₃), you can use the determinant method to calculate the area:
Area = ½ |(x₁(y₂ - y₃) + x₂(y₃ - y₁) + x₃(y₁ - y₂))|
The absolute value ensures a positive area.
Example 5: Area Calculation Using Coordinates
Consider a triangle with vertices A(1, 2), B(4, 6), and C(7, 2).
Area = ½ |(1(6 - 2) + 4(2 - 2) + 7(2 - 6))| = ½ |(4 + 0 - 28)| = ½ |-24| = 12 square units
Choosing the Right Method: A Practical Guide
The optimal method for calculating the area of a triangle depends entirely on the information available:
- Know base and height: Use the basic formula (½ * base * height). This is the simplest and most efficient method.
- Know all three sides: Use Heron's formula. This is particularly useful when the height isn't easily determined.
- Know two sides and the included angle: Use the trigonometric formula (½ * a * b * sin(C)). This method is efficient and accurate.
- Know the coordinates of the vertices: Use the determinant method from coordinate geometry. This is suitable for problems presented in coordinate systems.
Advanced Applications and Extensions
The concept of calculating triangle areas extends far beyond basic geometry problems. Here are some advanced applications:
1. Surveying and Land Measurement
Surveyors extensively utilize triangle area calculations to determine land areas accurately. They often use triangulation methods, breaking down larger land parcels into smaller triangles for easier measurement.
2. Computer Graphics and Image Processing
In computer graphics, triangles are fundamental building blocks for representing complex shapes and surfaces. Calculating the area of these triangles is crucial for rendering, texture mapping, and collision detection.
3. Engineering and Physics
Triangle area calculations are essential in various engineering disciplines, such as structural analysis, where they help determine the forces acting on triangular components. In physics, it's used in calculating work done by forces, centers of mass, and moments of inertia.
4. Data Analysis and Statistics
Triangle areas play a role in statistical analysis, particularly in visualizing data distributions and calculating probabilities within specific regions.
Conclusion: Mastering Triangle Area Calculations
Understanding how to calculate the area of a triangle is a cornerstone of mathematical and geometric understanding. While the basic formula provides a solid foundation, mastering the alternative methods – Heron's formula, trigonometric methods, and the coordinate geometry approach – unlocks a wider range of problem-solving capabilities. By selecting the appropriate method based on the given information and applying it accurately, you can confidently tackle various challenges across diverse fields. Remember to always double-check your calculations and consider the context of the problem to ensure accurate results. The ability to effectively determine the area of a triangle is a versatile skill that will serve you well in many areas of study and professional endeavors.
Latest Posts
Latest Posts
-
Food Is Digested Physical Or Chemical Change
Apr 08, 2025
-
Area Of A Triangle In 3d
Apr 08, 2025
-
Why Is Coal Not Considered A Mineral
Apr 08, 2025
-
Ecosystems Are Characterized By The Cycling Of
Apr 08, 2025
-
Which Of The Following Storage Units Is The Largest
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about What Is The Area Of The Triangle Shown . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.