What Is 60 Degrees In Radians
News Leon
Apr 05, 2025 · 4 min read
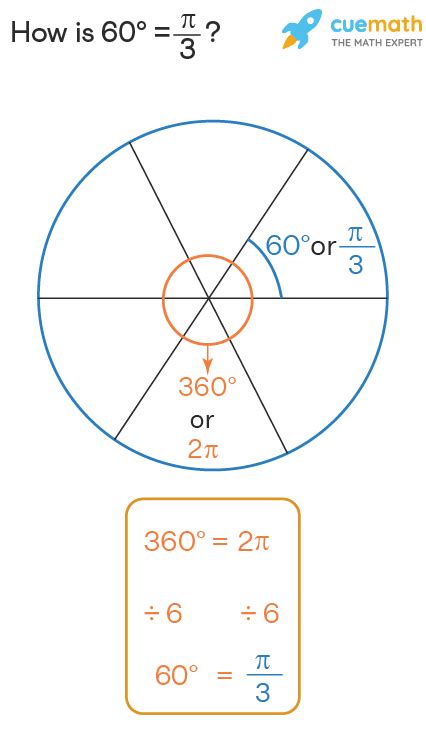
Table of Contents
What is 60 Degrees in Radians? A Comprehensive Guide
Degrees and radians are two common units for measuring angles. While degrees are more familiar in everyday life, radians are essential in many areas of mathematics, particularly calculus and trigonometry. Understanding the conversion between these units is crucial for anyone working with angles. This comprehensive guide will delve into the conversion of 60 degrees to radians, explaining the underlying concepts and providing practical examples.
Understanding Degrees and Radians
Before we jump into the conversion, let's establish a clear understanding of both units:
Degrees: A degree (°), denoted by the symbol °, is a unit of angular measurement defined as 1/360th of a full rotation around a circle. A full circle therefore contains 360 degrees. This system originated in ancient Babylonian mathematics, likely due to their base-60 number system.
Radians: A radian (rad), denoted by the symbol rad, is another unit of angular measurement. It's defined as the angle subtended at the center of a circle by an arc equal in length to the radius of the circle. This means if you take a circle and measure its radius, and then measure an arc along the circumference that is exactly the same length as the radius, the angle subtended at the center is one radian.
The Relationship Between Degrees and Radians
The key relationship between degrees and radians lies in the circumference of a circle. The circumference, C, of a circle with radius r is given by the formula:
C = 2πr
Since there are 360 degrees in a full circle, and the arc length of a full circle corresponds to 2π radians, we can establish the conversion factor:
360 degrees = 2π radians
Simplifying this, we get:
180 degrees = π radians
This fundamental relationship is the cornerstone of converting between degrees and radians.
Converting 60 Degrees to Radians
Now, let's apply this relationship to convert 60 degrees to radians. We can use the following proportion:
(degrees / 180°) = (radians / π)
Substituting 60 degrees for degrees, we get:
(60° / 180°) = (radians / π)
Simplifying the left side:
(1/3) = (radians / π)
Multiplying both sides by π gives us:
radians = (π/3)
Therefore, 60 degrees is equal to π/3 radians.
Understanding π/3 Radians
The value π/3 radians represents a significant angle in trigonometry. It's one of the "special angles" whose trigonometric functions (sine, cosine, tangent, etc.) have exact values, making them particularly useful in calculations.
To visualize π/3 radians:
- Recall that a full circle is 2π radians.
- Half a circle is π radians (180 degrees).
- π/3 radians is one-third of half a circle, or one-sixth of a full circle.
This corresponds to a 60-degree angle in a circle, forming an equilateral triangle when lines are drawn from the center to the endpoints of the arc.
Practical Applications of the Conversion
The conversion between degrees and radians is crucial in numerous applications, including:
1. Calculus:
Many calculus formulas involving angles are defined using radians. For instance, the derivative of sin(x) is cos(x) only when x is measured in radians. Using degrees would require an additional conversion factor, complicating the calculations.
2. Trigonometry:
Trigonometric functions like sine, cosine, and tangent are often more easily manipulated when angles are expressed in radians. Radians simplify many trigonometric identities and formulas.
3. Physics and Engineering:
In fields like physics and engineering, particularly in areas dealing with circular motion, rotational dynamics, and wave phenomena, radians are the preferred unit for angular measurement due to their mathematical elegance and ease of calculation. Formulas for angular velocity, angular acceleration, and other related quantities often involve radians directly.
4. Computer Graphics and Game Development:
Game engines and graphics libraries frequently use radians for representing angles and rotations. Understanding radian measure is thus essential for working with these technologies.
Common Conversions and Useful Tips
Remembering the basic conversion, 180 degrees = π radians, is key. From this, you can easily derive other conversions:
- 90 degrees = π/2 radians
- 45 degrees = π/4 radians
- 30 degrees = π/6 radians
- 15 degrees = π/12 radians
- And so on...
To convert from degrees to radians, multiply the angle in degrees by π/180.
To convert from radians to degrees, multiply the angle in radians by 180/π.
Advanced Concepts and Further Exploration
For a deeper understanding, you can explore:
- Unit Circle: Familiarize yourself with the unit circle, a visual representation that showcases the relationship between angles (in both degrees and radians) and the values of trigonometric functions.
- Taylor Series Expansions: Understanding how trigonometric functions can be represented using Taylor series will further demonstrate the advantages of using radians in calculus.
- Complex Numbers: Radians play a vital role in representing complex numbers in polar form.
Conclusion
Converting 60 degrees to π/3 radians is a straightforward process but represents a fundamental concept within mathematics and its applications. Understanding this conversion, coupled with a firm grasp of the relationship between degrees and radians, is essential for success in various scientific and technological fields. By mastering this conversion and exploring the deeper mathematical concepts related to radians, you'll gain a valuable skill set that will significantly enhance your understanding of mathematics and its applications in diverse areas. Remember to practice regularly to solidify your understanding and proficiency in converting between these essential angular units.
Latest Posts
Latest Posts
-
Which Of The Following Statements About Monsoons Are Correct
Apr 06, 2025
-
Provide An Acceptable Name For The Alkane Shown Below
Apr 06, 2025
-
Sulphuric Acid Reacts With Sodium Hydroxide
Apr 06, 2025
-
Which Of The Following Statements Regarding Lactose Tolerance Is True
Apr 06, 2025
-
What Is The Value Of Log7 343
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about What Is 60 Degrees In Radians . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
