True Or False Every Real Number Is A Rational Number
News Leon
Apr 05, 2025 · 5 min read
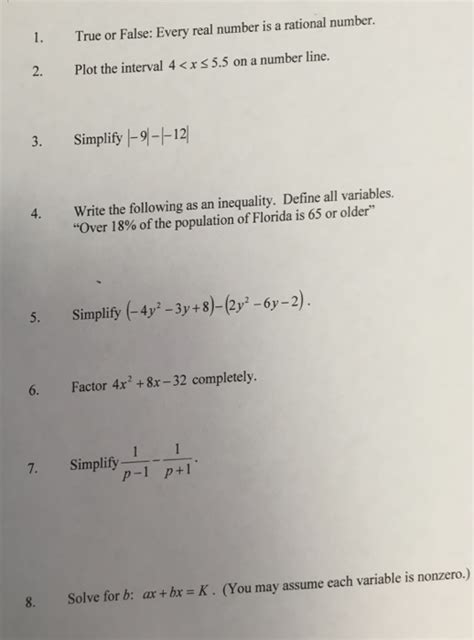
Table of Contents
True or False: Every Real Number is a Rational Number?
The statement "Every real number is a rational number" is false. This seemingly simple statement delves into the fundamental nature of numbers and requires a solid understanding of different number systems to fully grasp. Let's explore the world of real numbers, rational numbers, and irrational numbers to understand why this statement is incorrect.
Understanding Number Systems
Before diving into the veracity of our statement, let's establish a clear understanding of the different number systems involved:
Natural Numbers (Counting Numbers)
These are the numbers we use for counting: 1, 2, 3, 4, and so on. They are positive integers and form the foundation of many other number systems.
Whole Numbers
Whole numbers include natural numbers and zero (0). This simple addition expands our number set to encompass the absence of quantity.
Integers
Integers extend further to include negative whole numbers (-1, -2, -3, ...). This incorporates the concept of opposite quantities.
Rational Numbers
This is where things get more interesting. Rational numbers are numbers that can be expressed as a fraction p/q, where p and q are integers, and q is not zero. This definition encompasses many numbers:
- Integers: Any integer can be written as a fraction (e.g., 5 can be written as 5/1).
- Terminating Decimals: Decimals that end after a finite number of digits (e.g., 0.75 = 3/4).
- Repeating Decimals: Decimals with a repeating pattern of digits (e.g., 0.333... = 1/3).
Irrational Numbers
This is the key to understanding why the initial statement is false. Irrational numbers are real numbers that cannot be expressed as a fraction p/q, where p and q are integers, and q is not zero. Their decimal representations are non-terminating and non-repeating. Famous examples include:
- π (Pi): The ratio of a circle's circumference to its diameter, approximately 3.14159... Its digits continue infinitely without any repeating pattern.
- e (Euler's number): The base of the natural logarithm, approximately 2.71828... Like π, its decimal representation is infinite and non-repeating.
- √2 (Square root of 2): This number cannot be expressed as a fraction of integers. Its decimal representation is approximately 1.41421... and continues infinitely without repeating.
Real Numbers
Real numbers encompass both rational and irrational numbers. This is the complete set of numbers that can be plotted on a number line. They include all the number systems discussed above.
Why the Statement is False: The Existence of Irrational Numbers
The statement "Every real number is a rational number" is false because of the existence of irrational numbers. Irrational numbers are a subset of real numbers, but they cannot be expressed as fractions of integers. Since real numbers include both rational and irrational numbers, it's inaccurate to say that all real numbers are rational.
Imagine trying to represent π (pi) as a fraction. You can get close approximations (like 22/7), but you'll never find a fraction that perfectly equals π. This is the fundamental difference between rational and irrational numbers. Rational numbers can be perfectly represented as fractions, while irrational numbers cannot.
Visualizing the Relationship
Think of real numbers as a large circle. Inside this circle is a smaller circle representing rational numbers. The area outside the smaller circle, but still within the larger circle, represents irrational numbers. Because the larger circle (real numbers) contains the smaller circle (rational numbers) and the area outside it (irrational numbers), it is inaccurate to state that every element in the larger circle is also in the smaller circle.
Implications and Importance
Understanding the distinction between rational and irrational numbers has significant implications across various fields:
- Mathematics: The existence of irrational numbers expands the possibilities within mathematical calculations and proofs. Many important mathematical constants and relationships involve irrational numbers.
- Physics: Irrational numbers appear in numerous physical phenomena, such as the calculation of orbits, wave frequencies, and certain physical constants.
- Engineering: Engineers often deal with approximations of irrational numbers in their calculations, acknowledging the inherent limitations of representing them exactly.
- Computer Science: Representing irrational numbers in computers requires careful consideration of precision and rounding errors. Different approaches, such as floating-point arithmetic, are employed to handle these numbers effectively.
Examples of Irrational Numbers in Everyday Life (and their approximations)
While we might not use the precise value of π or √2 in everyday tasks, these numbers appear in various situations where approximations are sufficient:
- Calculating the area of a circle: We use π in the formula A = πr². While we use approximations like 3.14 or 22/7, the actual value of π is irrational.
- Measuring the diagonal of a square: If a square has sides of length 1, its diagonal length is √2. We can use an approximation like 1.414, but the precise value is irrational.
- Calculating the circumference of a circle: Similar to the area calculation, we use π in the formula C = 2πr. Again, approximations are used, but the precise circumference involves an irrational number.
Counterexamples: Proving the Statement False
To definitively prove the statement false, all we need is one counterexample – a single real number that is not rational. Any irrational number serves as a perfect counterexample:
- π (Pi): As discussed earlier, π is a real number but not a rational number. Its decimal representation is infinite and non-repeating.
- √2 (Square root of 2): This is another classic example of an irrational number, which is a real number but cannot be expressed as a fraction p/q.
- e (Euler's number): This fundamental mathematical constant is also irrational and thus a counterexample to the statement.
Conclusion: A Fundamental Distinction in Number Theory
The statement "Every real number is a rational number" is definitively false. The existence of irrational numbers, such as π, √2, and e, firmly establishes this. Understanding the distinction between rational and irrational numbers is crucial for grasping the fundamental structure of the real number system and its implications across various scientific and mathematical fields. While rational numbers can be precisely represented as fractions, irrational numbers defy such representation, revealing a richer and more complex landscape within the realm of numbers. This fundamental difference highlights the ongoing exploration and fascination surrounding the properties and behavior of numbers.
Latest Posts
Latest Posts
-
Which Of The Following Is Not A Characteristic Of Enzymes
Apr 06, 2025
-
Why Are Maps Important To Geographers
Apr 06, 2025
-
Google Search Console Crawl Reports Let You Monitor
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about True Or False Every Real Number Is A Rational Number . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
