True Or False All Whole Numbers Are Rational Numbers
News Leon
Apr 03, 2025 · 5 min read
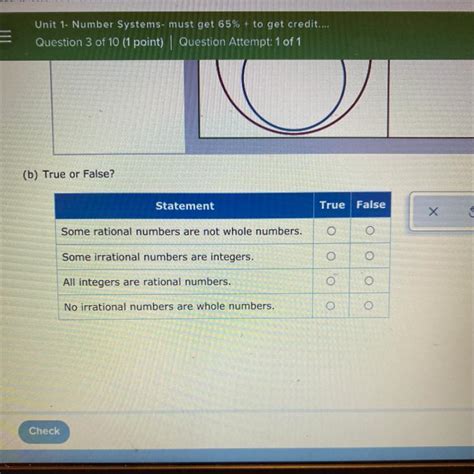
Table of Contents
True or False: All Whole Numbers are Rational Numbers
The question, "Are all whole numbers rational numbers?" is a fundamental one in mathematics, touching upon the core definitions of these number systems. The short answer is true. However, to fully understand why, we need to delve deeper into the definitions of whole numbers and rational numbers, exploring their properties and relationships. This exploration will solidify your understanding and equip you with the knowledge to confidently answer similar questions about different number sets.
Understanding Whole Numbers
Whole numbers are the foundation of our number system. They begin with zero and continue infinitely in the positive direction. Think of them as the numbers you use for counting discrete objects. The set of whole numbers is typically represented by the symbol W and can be written as:
W = {0, 1, 2, 3, 4, 5, ...}
These numbers are non-negative and do not include fractions or decimals. They are the building blocks upon which more complex number systems are built. Understanding their characteristics is crucial for comprehending higher-level mathematical concepts.
Key Characteristics of Whole Numbers:
- Non-negative: Whole numbers are always greater than or equal to zero. Negative numbers are not included.
- Integers: Whole numbers form a subset of the integers (all positive and negative whole numbers and zero).
- Discrete: Whole numbers represent distinct, separate quantities. There are no values between consecutive whole numbers.
- Counting: Whole numbers are used for counting objects and measuring quantities in discrete units.
Understanding Rational Numbers
Rational numbers represent a significant expansion beyond whole numbers. They encompass all numbers that can be expressed as a fraction where the numerator and denominator are both integers, and the denominator is not zero. This definition introduces the concept of fractions and decimals, greatly expanding the range of numbers we can work with. The set of rational numbers is often denoted by the symbol Q.
Q = {p/q | p, q ∈ Z, q ≠ 0}
where 'p' and 'q' are integers, and 'q' (the denominator) is not zero.
Key Characteristics of Rational Numbers:
- Fractions: Rational numbers can be expressed as fractions – a ratio of two integers.
- Decimals: Rational numbers can also be expressed as terminating or repeating decimals. A terminating decimal is one that ends (e.g., 0.25), and a repeating decimal has a digit or sequence of digits that repeats infinitely (e.g., 0.333...).
- Integers are included: All integers (positive, negative, and zero) are rational numbers because they can be expressed as fractions (e.g., 5 can be written as 5/1).
- Density: Between any two rational numbers, there exists another rational number. This property is known as density.
Connecting Whole Numbers and Rational Numbers
Now that we've clearly defined both whole numbers and rational numbers, let's explore their relationship. The key to understanding why all whole numbers are rational lies in the definition of rational numbers: any number that can be expressed as a fraction p/q, where p and q are integers, and q ≠ 0.
Consider any whole number, for example, 7. Can this be expressed as a fraction? Absolutely! We can write 7 as 7/1. Here, both 7 and 1 are integers, and the denominator is not zero. This fulfills the definition of a rational number.
Let's take another example, the whole number 0. This can be expressed as 0/1, 0/2, 0/3, and so on. Again, this satisfies the definition of a rational number.
This pattern holds true for all whole numbers. Every whole number can be written as a fraction with the whole number as the numerator and 1 as the denominator. Since this satisfies the definition of a rational number, it follows that all whole numbers are rational numbers.
Visualizing the Relationship
To further solidify this concept, consider a Venn diagram. The set of whole numbers (W) is entirely contained within the set of rational numbers (Q). This visual representation clearly shows that all whole numbers are a subset of rational numbers, reinforcing the truth of our statement.
Beyond Whole and Rational Numbers: Other Number Systems
Understanding the relationship between whole and rational numbers provides a foundation for understanding other number sets within the broader landscape of mathematics:
1. Integers (Z):**
Integers include all whole numbers and their negative counterparts. Z = {..., -3, -2, -1, 0, 1, 2, 3, ...}. Like whole numbers, all integers are also rational numbers.
2. Irrational Numbers:**
Irrational numbers are numbers that cannot be expressed as a fraction of two integers. They have non-terminating and non-repeating decimal expansions. Famous examples include π (pi) and √2 (the square root of 2).
3. Real Numbers (R):**
Real numbers encompass all rational and irrational numbers. They represent all points on the number line.
Practical Applications and Importance
The understanding that all whole numbers are rational numbers is not just a theoretical concept; it has practical implications across various fields:
- Computer Science: Many algorithms and data structures rely on the properties of rational numbers, and the ability to represent whole numbers as rational numbers is fundamental to these operations.
- Engineering: In engineering calculations, especially those involving fractions and ratios, understanding the relationship between whole and rational numbers is crucial for accuracy and precision.
- Finance: Financial calculations often involve fractions (e.g., interest rates, percentages), and the ability to represent whole numbers as rational numbers is essential in these computations.
Conclusion: A Foundation for Further Learning
The assertion that all whole numbers are rational numbers is demonstrably true. By carefully examining the definitions of whole numbers and rational numbers, and understanding their properties, we can conclusively establish this relationship. This understanding serves as a crucial stepping stone for further explorations into more complex number systems and their applications in various fields. Mastering these fundamental concepts is essential for success in advanced mathematics and related disciplines. Remember, a solid grasp of foundational mathematical concepts empowers you to confidently tackle more complex problems and expands your capacity for critical thinking and problem-solving.
Latest Posts
Latest Posts
-
Collection Of Similar Cells That Perform A Particular Function
Apr 03, 2025
-
Which Atomic Particle Determines The Chemical Behavior Of An Atom
Apr 03, 2025
-
Which Of The Following Occurs First Causing Expiration
Apr 03, 2025
-
A Homogeneous Mixture Is Also Called A
Apr 03, 2025
-
Least Common Multiple Of 3 6 9
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about True Or False All Whole Numbers Are Rational Numbers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
