The Instantaneous Velocity Of An Object Is The
News Leon
Apr 07, 2025 · 6 min read
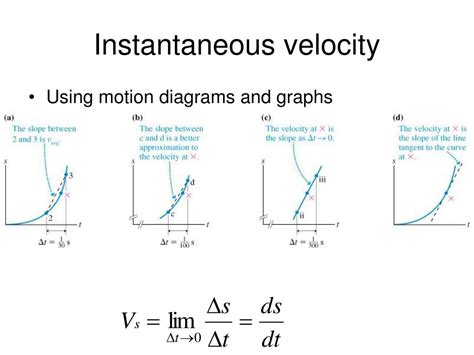
Table of Contents
The Instantaneous Velocity of an Object Is... a Deep Dive into Calculus and Motion
Understanding motion is fundamental to physics. While average velocity provides a broad overview of movement over a period, it fails to capture the nuances of an object's speed and direction at any precise moment. This is where the concept of instantaneous velocity shines. This article will explore the intricacies of instantaneous velocity, its relationship to average velocity, and its crucial role in understanding the dynamics of moving objects. We'll delve into the mathematical underpinnings, provide practical examples, and highlight its significance in various scientific fields.
Understanding Average Velocity
Before delving into the complexities of instantaneous velocity, let's revisit the simpler concept of average velocity. Average velocity is defined as the total displacement of an object divided by the total time taken. Displacement, unlike distance, is a vector quantity, meaning it has both magnitude (size) and direction. It represents the straight-line distance between the object's starting and ending points, regardless of the path taken.
Formula for Average Velocity:
Average Velocity (v<sub>avg</sub>) = Δx / Δt
Where:
- Δx represents the change in displacement (final displacement - initial displacement)
- Δt represents the change in time (final time - initial time)
Example: If a car travels 100 kilometers east in 2 hours, its average velocity is 50 kilometers per hour east. Note that the direction (east) is crucial as it defines the vector nature of velocity.
The Limitations of Average Velocity
Average velocity, while useful in many situations, provides a limited picture of motion. Consider a car accelerating from a standstill. Its average velocity over, say, the first 10 seconds might be 15 m/s. However, this average doesn't reflect the fact that the car's speed was initially zero and gradually increased to a higher value. The average velocity masks the variations in speed during that 10-second interval. This is precisely where instantaneous velocity comes into play.
Introducing Instantaneous Velocity: A Snapshot in Time
Instantaneous velocity is the velocity of an object at a specific instant in time. It represents the rate of change of the object's displacement at that exact moment. Unlike average velocity, which considers motion over a time interval, instantaneous velocity focuses on a single point in time. Imagine taking a photograph of a moving car – the snapshot captures its position and speed at that very moment; this is analogous to instantaneous velocity.
Key Difference: Average velocity is concerned with the overall change in displacement over a duration, while instantaneous velocity focuses on the rate of change of displacement at a specific point within that duration.
The Calculus Connection: Derivatives and Instantaneous Velocity
The mathematical concept of the derivative from calculus is essential for calculating instantaneous velocity. The derivative of a displacement-time function provides the instantaneous rate of change of displacement with respect to time, which is precisely the instantaneous velocity.
Let's assume the displacement of an object is described by a function x(t). Then, the instantaneous velocity v(t) at time t is given by:
Formula for Instantaneous Velocity:
v(t) = dx(t)/dt
This equation represents the derivative of the displacement function x(t) with respect to time t. This derivative describes the slope of the tangent line to the displacement-time graph at the specific time t. The slope of this tangent line represents the instantaneous rate of change of displacement – the instantaneous velocity.
Graphical Representation: Understanding the Tangent Line
Consider a graph plotting displacement (x) on the vertical axis and time (t) on the horizontal axis. The average velocity between two points on this graph is represented by the slope of the secant line connecting those points. However, the instantaneous velocity at a specific point is represented by the slope of the tangent line to the curve at that point. As the time interval approaches zero, the secant line approaches the tangent line, and the average velocity approaches the instantaneous velocity.
Calculating Instantaneous Velocity: Examples
Let's illustrate with some examples:
Example 1: Constant Velocity
If an object moves with constant velocity, its displacement function is linear: x(t) = vt + x₀, where v is the constant velocity and x₀ is the initial displacement. The derivative of this function, and hence the instantaneous velocity, is simply v. This confirms that for constant velocity motion, the instantaneous velocity is always equal to the average velocity.
Example 2: Uniformly Accelerated Motion
Consider an object undergoing uniformly accelerated motion, where its displacement is given by: x(t) = 1/2at² + v₀t + x₀ (where a is constant acceleration, v₀ is initial velocity and x₀ is initial displacement). The instantaneous velocity is the derivative: v(t) = at + v₀. This shows that the instantaneous velocity changes linearly with time in uniformly accelerated motion.
Example 3: Non-Uniform Motion
For more complex motion where the acceleration isn't constant, the displacement function will be more intricate. For instance, consider x(t) = t³ - 6t² + 9t. The instantaneous velocity is found by taking the derivative: v(t) = 3t² - 12t + 9. This equation allows us to calculate the instantaneous velocity at any specific time t.
Instantaneous Velocity in Different Fields
The concept of instantaneous velocity extends far beyond theoretical physics. It finds practical applications in various fields:
-
Engineering: Designing vehicles, aircraft, and other moving systems requires precise knowledge of instantaneous velocity for control and stability.
-
Robotics: Precise control of robotic arms and other robotic systems relies on calculating and adjusting instantaneous velocity.
-
Sports Science: Analyzing the motion of athletes, such as runners or swimmers, involves determining their instantaneous velocity at different points in their performance.
-
Meteorology: Tracking weather patterns and predicting the movement of storms relies on calculating the instantaneous velocity of air masses.
Beyond Velocity: Instantaneous Acceleration
Building upon the concept of instantaneous velocity, we can extend the idea to instantaneous acceleration. Instantaneous acceleration is the rate of change of instantaneous velocity at a specific instant. It's the derivative of the velocity function with respect to time: a(t) = dv(t)/dt = d²x(t)/dt². This second derivative provides a precise measure of how the velocity is changing at any given moment.
Conclusion: The Essence of Instantaneous Velocity
Instantaneous velocity, a seemingly abstract concept from calculus, provides a powerful tool for understanding and analyzing motion. It moves beyond the limitations of average velocity by providing a precise measure of an object's speed and direction at any given moment. Its applications extend across numerous scientific and engineering disciplines, emphasizing its importance in understanding the dynamic world around us. By understanding instantaneous velocity and its mathematical foundation, we gain a deeper appreciation for the complexities and precision involved in describing motion. Further exploration into more advanced concepts like vectors, relative velocity, and curvilinear motion will build upon this foundational understanding, leading to a more complete grasp of kinematics and dynamics.
Latest Posts
Latest Posts
-
Find The Geometric Mean Of 9 And 16
Apr 08, 2025
-
Can A Compound Be Separated By Physical Means
Apr 08, 2025
-
Find The Magnitude Of The Electric Dipole Moment
Apr 08, 2025
-
Log 1 Log 2 Log 3
Apr 08, 2025
-
What Part Of The Cell Transports Materials Within The Cell
Apr 08, 2025
Related Post
Thank you for visiting our website which covers about The Instantaneous Velocity Of An Object Is The . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.