The Distance Around A Figure Is The
News Leon
Apr 03, 2025 · 5 min read
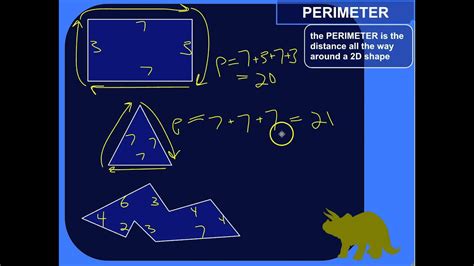
Table of Contents
The Distance Around a Figure is the Perimeter: A Comprehensive Guide
The distance around a figure is formally known as its perimeter. Understanding perimeter is fundamental in various fields, from everyday life to advanced mathematics and engineering. This comprehensive guide will delve deep into the concept of perimeter, exploring its definition, calculation methods for different shapes, real-world applications, and even touch upon related mathematical concepts.
What is Perimeter?
Simply put, the perimeter of a two-dimensional (2D) shape is the total length of its boundary. Imagine an ant walking around the edges of a shape; the total distance it travels is the perimeter. This concept applies to all closed shapes, regardless of their complexity. It's a crucial measurement used in various contexts, from calculating the amount of fencing needed for a yard to determining the length of track needed for a race.
Key Terminology:
Before diving deeper, let's clarify some crucial terms:
- 2D Shape: A flat shape with two dimensions: length and width. Examples include squares, circles, triangles, rectangles, and more complex polygons.
- Boundary: The outer edge or line forming the shape.
- Length: The measurement of one side of a shape.
- Units: The units used to measure perimeter (e.g., centimeters, meters, inches, feet, kilometers, miles). Always remember to include the unit in your final answer.
Calculating Perimeter for Different Shapes
Calculating the perimeter depends on the shape's type. Here's a breakdown for common shapes:
1. Squares and Rectangles
Squares and rectangles are the simplest shapes to work with. Their perimeters are calculated using straightforward formulas:
-
Square: A square has four equal sides. The perimeter (P) is calculated as:
P = 4s, where 's' is the length of one side. -
Rectangle: A rectangle has two pairs of equal sides (length and width). The perimeter (P) is calculated as:
P = 2(l + w), where 'l' is the length and 'w' is the width.
Example: A square with sides of 5 cm has a perimeter of 4 * 5 cm = 20 cm. A rectangle with a length of 8 meters and a width of 6 meters has a perimeter of 2 * (8m + 6m) = 28 meters.
2. Triangles
Triangles, with their three sides, require a slightly different approach:
- Perimeter of a Triangle: The perimeter (P) is the sum of the lengths of all three sides:
P = a + b + c, where 'a', 'b', and 'c' represent the lengths of the three sides.
Example: A triangle with sides of 3 inches, 4 inches, and 5 inches has a perimeter of 3 inches + 4 inches + 5 inches = 12 inches.
3. Circles
Circles present a unique challenge because they don't have straight sides. Instead, we use the concept of circumference, which is the perimeter of a circle.
- Circumference of a Circle: The circumference (C) is calculated using the formula:
C = 2πr, where 'r' is the radius of the circle (the distance from the center to any point on the circle), and π (pi) is a mathematical constant approximately equal to 3.14159. Alternatively, you can use the diameter (d), which is twice the radius:C = πd.
Example: A circle with a radius of 7 cm has a circumference of 2 * π * 7 cm ≈ 43.98 cm.
4. Irregular Polygons
For polygons with more than four sides and irregular side lengths (meaning the sides are not all equal), the perimeter is simply the sum of the lengths of all its sides. Carefully measure each side and add them together.
Example: An irregular pentagon with sides measuring 2, 3, 4, 5, and 6 units has a perimeter of 2 + 3 + 4 + 5 + 6 = 20 units.
Real-World Applications of Perimeter
The concept of perimeter extends far beyond theoretical mathematics. It finds practical applications in numerous real-world scenarios:
- Construction and Architecture: Calculating the amount of materials needed for fencing, building walls, or laying flooring.
- Landscaping: Determining the length of fencing needed to enclose a garden or yard.
- Sports: Measuring the length of running tracks, swimming pools, or playing fields.
- Engineering: Designing structures with specific boundary dimensions.
- Art and Design: Creating designs with precise perimeter measurements.
- Sewing and Fabric Cutting: Determining the amount of fabric needed for garments or other projects.
- Cartography: Calculating distances between locations on maps.
Advanced Concepts Related to Perimeter
While the basic concept of perimeter is straightforward, it connects to more advanced mathematical concepts:
1. Area vs. Perimeter
It's crucial to distinguish between perimeter and area. Perimeter measures the distance around a shape, while area measures the space inside the shape. These are two distinct concepts that shouldn't be confused. For instance, two shapes can have the same perimeter but different areas, or vice versa.
2. Isoperimetric Problem
The isoperimetric problem explores the question: For a given perimeter, what shape encloses the maximum area? The solution, proven mathematically, is the circle. This principle has implications in various fields, from biology (cell structures) to engineering (efficient designs).
3. Geometry and Trigonometry
Perimeter calculations often involve geometric principles and, in some cases, trigonometry, particularly when dealing with irregular shapes or shapes involving angles. Understanding these concepts is essential for accurate perimeter calculations in complex scenarios.
4. Calculus and Curves
For complex curves, calculating the perimeter might require the use of calculus, specifically integration techniques, to find the arc length along the curve.
Tips for Accurate Perimeter Calculations
To ensure accuracy when calculating perimeter:
- Use Consistent Units: Maintain consistent units throughout your calculations. Don't mix centimeters and meters, for example.
- Accurate Measurements: Use precise measuring tools to obtain accurate measurements of the sides of shapes.
- Break Down Complex Shapes: If dealing with a complex shape, break it down into simpler shapes (e.g., rectangles and triangles) to calculate the perimeter of each part and then add them together.
- Formula Familiarity: Ensure you are familiar with the correct formulas for different shapes.
- Check Your Work: Always double-check your calculations to prevent errors.
Conclusion
Understanding perimeter is a fundamental skill with wide-ranging applications. This guide has provided a comprehensive overview of the concept, calculation methods, real-world uses, and its connections to more advanced mathematical concepts. Mastering the concept of perimeter enhances problem-solving abilities in various contexts, making it a valuable tool in numerous fields. Remember to always be mindful of units and double-check your calculations for accuracy. By understanding and applying the principles outlined here, you can confidently tackle perimeter problems in any scenario.
Latest Posts
Latest Posts
-
Curdling Of Milk Is A Chemical Change
Apr 04, 2025
-
Paleolithic Age Is Also Known As The
Apr 04, 2025
-
What Is Found In Both Eukaryotic And Prokaryotic Cells
Apr 04, 2025
-
Select The Correct Electron Configuration For Cr
Apr 04, 2025
-
Can A Pure Substance Be A Compound
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about The Distance Around A Figure Is The . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
