Sin 2 Cos 2 1 Proof
News Leon
May 05, 2025 · 5 min read
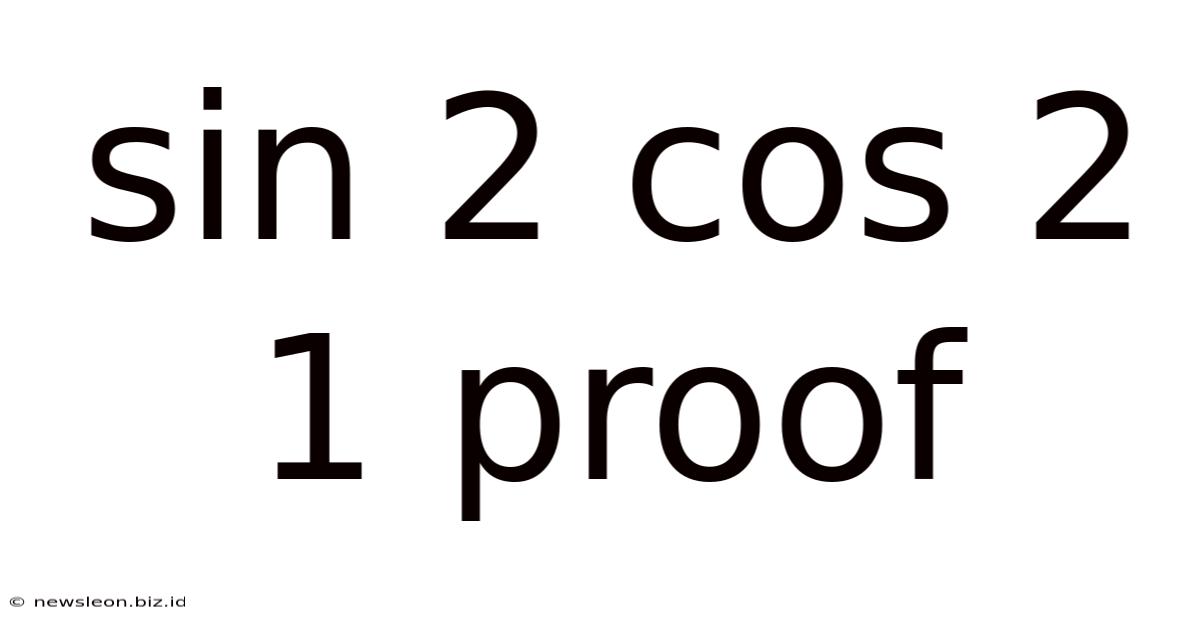
Table of Contents
Sin²x + Cos²x = 1: A Comprehensive Proof and its Applications
The trigonometric identity sin²x + cos²x = 1 is a fundamental relationship in mathematics, particularly within trigonometry and calculus. Understanding its proof and applications is crucial for anyone studying these fields. This article will delve deep into the proof of this identity, exploring various methods and highlighting its significance across different mathematical contexts. We’ll also explore some of its important corollaries and applications.
Understanding the Unit Circle
Before diving into the proofs, let's establish a foundational understanding of the unit circle. The unit circle is a circle with a radius of 1 centered at the origin (0,0) on a Cartesian coordinate system. Any point (x, y) on the unit circle can be represented using trigonometric functions:
- x = cos θ
- y = sin θ
where θ is the angle formed by the positive x-axis and the line segment connecting the origin to the point (x, y).
This representation is key to visually understanding and proving the identity sin²x + cos²x = 1.
Proof 1: Using the Pythagorean Theorem
This is perhaps the most common and intuitive proof. Consider a right-angled triangle inscribed within the unit circle. The hypotenuse of this triangle is the radius of the unit circle, which has a length of 1. The legs of the triangle have lengths corresponding to the x and y coordinates of the point on the circle.
- Hypotenuse = 1
- Adjacent side = cos θ
- Opposite side = sin θ
Applying the Pythagorean theorem (a² + b² = c²) to this triangle, we get:
(cos θ)² + (sin θ)² = 1²
Simplifying, we arrive at the desired identity:
sin²θ + cos²θ = 1
This proof directly connects the trigonometric functions to the geometric properties of the right-angled triangle and the unit circle, offering a clear and visually appealing demonstration.
Proof 2: Using Trigonometric Definitions
This proof leverages the definitions of sine and cosine in terms of the coordinates of a point on the unit circle.
Recall that for a point (x, y) on the unit circle at angle θ:
- cos θ = x / r where r is the radius (which is 1 in the unit circle)
- sin θ = y / r where r is the radius (which is 1 in the unit circle)
Therefore, in a unit circle:
- cos θ = x
- sin θ = y
The equation of the unit circle is x² + y² = 1. Substituting the trigonometric definitions, we get:
(cos θ)² + (sin θ)² = 1
sin²θ + cos²θ = 1
This proof elegantly uses the algebraic definition of the unit circle to derive the trigonometric identity.
Proof 3: Using Euler's Formula
This proof utilizes Euler's formula, a fundamental result in complex analysis that connects exponential functions to trigonometric functions:
e^(iθ) = cos θ + i sin θ
where 'i' is the imaginary unit (√-1).
Taking the complex conjugate:
e^(-iθ) = cos θ - i sin θ
Now, multiply the two equations:
e^(iθ) * e^(-iθ) = (cos θ + i sin θ)(cos θ - i sin θ)
Simplifying the left side using exponent rules:
e^(iθ - iθ) = e⁰ = 1
Expanding the right side:
cos²θ - (i sin θ)² = cos²θ + sin²θ (since i² = -1)
Therefore:
sin²θ + cos²θ = 1
This proof demonstrates the power of complex analysis in deriving fundamental trigonometric identities. It showcases the deep connections between seemingly disparate areas of mathematics.
Applications of sin²x + cos²x = 1
The identity sin²x + cos²x = 1 has widespread applications across various mathematical disciplines. Here are a few examples:
1. Simplifying Trigonometric Expressions:
This identity is frequently used to simplify complex trigonometric expressions. For example, you can use it to rewrite expressions involving both sine and cosine into a single trigonometric function.
Consider an expression like: 3sin²x + 3cos²x. Using the identity, this simplifies to 3(sin²x + cos²x) = 3(1) = 3.
2. Deriving Other Trigonometric Identities:
The fundamental identity serves as a cornerstone for deriving many other important trigonometric identities. By dividing both sides of the equation by either sin²x or cos²x, we can derive identities involving tangent, cotangent, secant, and cosecant functions.
For instance, dividing by cos²x gives:
tan²x + 1 = sec²x
Dividing by sin²x gives:
1 + cot²x = csc²x
These derived identities are incredibly useful in solving various trigonometric problems.
3. Calculus:
In calculus, the identity plays a crucial role in simplifying derivatives and integrals of trigonometric functions. It is often used to rewrite expressions before applying integration techniques like substitution or integration by parts.
For example, when integrating expressions involving powers of sine and cosine, the identity can help manipulate the integrand into a more manageable form.
4. Physics and Engineering:
The identity finds applications in numerous areas of physics and engineering, where trigonometric functions are used to model oscillations, waves, and rotations. It appears in calculations involving simple harmonic motion, alternating current circuits, and wave phenomena.
5. Computer Graphics:
In computer graphics, trigonometric functions are essential for representing rotations and transformations. The identity sin²x + cos²x = 1 is implicitly used in many algorithms and calculations related to these transformations.
Corollaries and Variations
The fundamental identity has several important corollaries that are derived directly from it:
- sin²x = 1 - cos²x
- cos²x = 1 - sin²x
These variations prove incredibly helpful when solving equations or simplifying expressions involving sine and cosine.
Conclusion
The trigonometric identity sin²x + cos²x = 1 stands as a fundamental pillar of trigonometry and its applications. Its elegant proof using various methods—the Pythagorean theorem, trigonometric definitions, and even Euler's formula—highlights the interconnectedness of different mathematical concepts. Its extensive use in simplifying expressions, deriving other identities, and solving problems in diverse fields such as calculus, physics, and computer graphics underscores its profound importance in mathematics and beyond. Mastering this identity and its associated proofs and corollaries is a crucial step for anyone pursuing deeper studies in mathematics or related scientific disciplines. Understanding its geometric and algebraic interpretations further enhances its versatility and allows for a more intuitive grasp of trigonometric concepts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Sin 2 Cos 2 1 Proof . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.