Simplify 3 Square Root Of 125
News Leon
May 03, 2025 · 4 min read
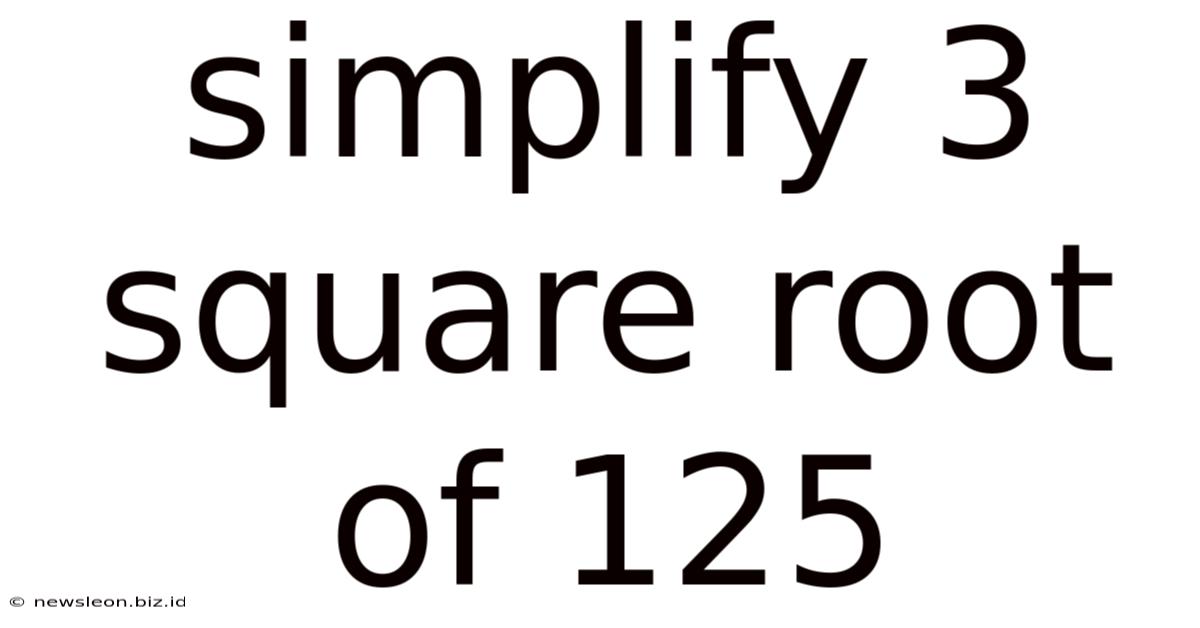
Table of Contents
Simplifying the Cube Root of 125: A Comprehensive Guide
The seemingly simple task of simplifying the cube root of 125 offers a fantastic opportunity to delve into the fundamentals of simplifying radicals and explore the broader concepts of prime factorization and exponential notation. This comprehensive guide will not only show you how to simplify ³√125 but also equip you with the knowledge and skills to tackle similar problems with confidence. We'll explore various methods, address common misconceptions, and provide plenty of practice examples to solidify your understanding.
Understanding Cube Roots and Radicals
Before we tackle the simplification of ³√125, let's establish a firm understanding of what cube roots and radicals represent.
A radical is a mathematical expression that uses a radical symbol (√) to denote a root of a number. The number inside the radical symbol is called the radicand. The small number placed above and to the left of the radical symbol is the index, indicating the root being taken. For example, in √x, the index is 2 (implied, as it's a square root), and x is the radicand. In ³√x, the index is 3 (cube root), and x is the radicand.
A cube root is a number that, when multiplied by itself three times, results in the original number. In other words, if x³ = y, then ³√y = x.
Method 1: Prime Factorization
The most reliable and generally applicable method for simplifying cube roots is through prime factorization. This method breaks down the radicand into its prime factors. Let's apply this to our example, ³√125:
-
Find the prime factorization of 125: We can break down 125 as follows:
125 = 5 x 25 = 5 x 5 x 5 = 5³
-
Rewrite the cube root using prime factors: Now, we can rewrite ³√125 as ³√(5³).
-
Simplify the cube root: Since we are taking the cube root, and we have a perfect cube (5³), we can simplify the expression:
³√(5³) = 5
Therefore, the simplified form of ³√125 is 5.
Method 2: Using Perfect Cubes
This method relies on recognizing perfect cubes within the radicand. A perfect cube is a number that is the result of cubing an integer (e.g., 1³, 2³, 3³, etc.).
-
Identify perfect cubes: We need to see if 125 is a perfect cube or contains a perfect cube as a factor. Since 5³ = 125, 125 is a perfect cube.
-
Simplify: Because 125 is 5 cubed, the cube root of 125 is simply 5.
³√125 = ³√(5³) = 5
Understanding the Relationship Between Cubes and Cube Roots
It's crucial to understand the inverse relationship between cubing a number and taking its cube root. Cubing a number means multiplying it by itself three times, while taking the cube root is the reverse operation: finding the number that, when cubed, gives the original number.
For example:
- 2³ = 2 x 2 x 2 = 8
- ³√8 = 2
Simplifying Cube Roots with Non-Perfect Cubes
Not all cube roots result in whole numbers. Let's consider a slightly more complex example: ³√216
-
Prime Factorization:
216 = 2 x 108 = 2 x 2 x 54 = 2 x 2 x 2 x 27 = 2 x 2 x 2 x 3 x 9 = 2 x 2 x 2 x 3 x 3 x 3 = 2³ x 3³
-
Rewrite and Simplify:
³√216 = ³√(2³ x 3³) = ³√2³ x ³√3³ = 2 x 3 = 6
Simplifying Cube Roots with Variables
The principles of prime factorization and perfect cubes extend to expressions involving variables. Let's consider an example: ³√(8x³y⁶)
-
Prime Factorization and Exponential Properties:
³√(8x³y⁶) = ³√(2³x³y⁶)
-
Simplify:
³√(2³x³y⁶) = ³√2³ x ³√x³ x ³√y⁶ = 2xy² (Note: y⁶ = (y²)³ )
Common Mistakes to Avoid
Several common mistakes can hinder the simplification process:
- Incorrect prime factorization: Ensure you completely break down the radicand into its prime factors.
- Confusing square roots and cube roots: Remember the index dictates the type of root being taken.
- Improper application of exponent rules: Ensure your understanding of exponent rules is solid.
- Forgetting to simplify completely: Always check if further simplification is possible.
Practice Problems
To reinforce your understanding, try simplifying the following cube roots:
- ³√64
- ³√729
- ³√(27x⁹)
- ³√(1000a⁶b³)
- ³√(1728m¹²n¹⁵)
Solutions:
- ³√64 = 4 (4³ = 64)
- ³√729 = 9 (9³ = 729)
- ³√(27x⁹) = 3x³
- ³√(1000a⁶b³) = 10a²b
- ³√(1728m¹²n¹⁵) = 12m⁴n⁵
Conclusion: Mastering Cube Root Simplification
Simplifying cube roots, while seemingly straightforward, provides a solid foundation in algebraic manipulation and number theory. By mastering prime factorization, understanding perfect cubes, and applying the relevant exponent rules, you can confidently tackle a wide range of radical expressions. Remember to practice regularly, identify and avoid common mistakes, and use various methods to solve problems effectively. This will not only improve your mathematical skills but also enhance your problem-solving abilities in a broader context. The journey from ³√125 = 5 is just the beginning of a much larger mathematical exploration.
Latest Posts
Related Post
Thank you for visiting our website which covers about Simplify 3 Square Root Of 125 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.