Si Unit For Moment Of Inertia
News Leon
Apr 04, 2025 · 6 min read
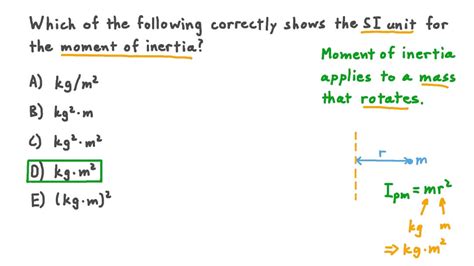
Table of Contents
SI Units for Moment of Inertia: A Comprehensive Guide
Moment of inertia, a crucial concept in physics and engineering, quantifies an object's resistance to changes in its rotation. Understanding its SI unit is fundamental to accurately calculating rotational motion and related properties. This comprehensive guide delves deep into the SI unit for moment of inertia, exploring its derivation, applications, and practical implications. We'll also touch upon related concepts and provide examples to solidify your understanding.
Understanding Moment of Inertia
Before diving into the units, let's establish a solid understanding of moment of inertia itself. It's a measure of how difficult it is to change the rotational speed of a rotating object. Unlike mass, which resists linear acceleration, moment of inertia resists angular acceleration. The distribution of mass relative to the axis of rotation is the key factor. A mass concentrated further from the axis of rotation contributes more significantly to the moment of inertia than a similar mass closer to the axis.
Think of it this way: Imagine trying to spin a bicycle wheel versus a solid disc of the same mass. The wheel, with its mass concentrated at the rim, will be much harder to spin up to a certain speed than the solid disc, because it has a greater moment of inertia.
The SI Unit: Kilogram-meter squared (kg⋅m²)
The SI unit for moment of inertia is the kilogram-meter squared (kg⋅m²). This unit directly reflects the physical definition of moment of inertia. Let's break down why:
-
Kilogram (kg): This represents the mass of the object. As mentioned, the distribution of mass is critical in determining moment of inertia. More mass means more resistance to changes in rotation.
-
Meter squared (m²): This represents the square of the distance of the mass from the axis of rotation. The further the mass is from the axis, the larger the value of m², and consequently, the larger the moment of inertia. The square relationship emphasizes the significant impact of distance. Doubling the distance quadruples the contribution to the moment of inertia.
This combination of mass and distance squared perfectly captures the essence of moment of inertia: the resistance to changes in rotational motion.
Calculating Moment of Inertia: Different Shapes and Approaches
Calculating the moment of inertia depends heavily on the shape of the object and the chosen axis of rotation. For simple shapes, we have established formulas. For more complex shapes, integration techniques are necessary.
Simple Shapes: Formulas and Examples
-
Thin Rod about its Center: I = (1/12)ML², where M is the mass and L is the length of the rod.
-
Thin Rod about its End: I = (1/3)ML²
-
Solid Cylinder or Disc about its Central Axis: I = (1/2)MR², where M is the mass and R is the radius.
-
Solid Sphere about its Diameter: I = (2/5)MR², where M is the mass and R is the radius.
-
Hollow Cylinder or Ring about its Central Axis: I = MR², where M is the mass and R is the radius.
Example: Consider a solid cylinder with a mass of 2 kg and a radius of 0.5 meters. Its moment of inertia about its central axis would be:
I = (1/2)MR² = (1/2) * 2 kg * (0.5 m)² = 0.25 kg⋅m²
This means the cylinder's resistance to rotational acceleration is 0.25 kg⋅m².
Complex Shapes: Integration Techniques
For irregularly shaped objects, calculating the moment of inertia requires integration. The general formula involves summing the contributions of infinitesimally small mass elements:
I = ∫r²dm
Where:
Iis the moment of inertiaris the perpendicular distance of the mass elementdmfrom the axis of rotationdmis an infinitesimally small mass element- The integral is taken over the entire volume of the object.
This integral can be quite challenging depending on the object's shape and mass distribution, often requiring advanced calculus techniques.
Parallel Axis Theorem: Shifting the Axis of Rotation
The parallel axis theorem provides a powerful shortcut. It allows us to calculate the moment of inertia about an axis parallel to an axis passing through the center of mass, given the moment of inertia about the center of mass.
The theorem states:
I = I<sub>cm</sub> + Md²
Where:
Iis the moment of inertia about the parallel axisI<sub>cm</sub>is the moment of inertia about the center of massMis the total mass of the objectdis the distance between the two parallel axes.
This theorem significantly simplifies calculations, especially when dealing with objects rotated about an axis that doesn't pass through their center of mass.
Applications of Moment of Inertia and its Unit
The moment of inertia and its unit, kg⋅m², are vital across numerous fields:
-
Rotational Dynamics: Understanding the moment of inertia is crucial for analyzing the rotational motion of objects, including calculating angular acceleration, torque, and angular momentum.
-
Engineering Design: Engineers use moment of inertia calculations in designing rotating machinery, vehicles, and structures to ensure stability and performance. For example, the design of flywheels, which are used for energy storage, depends heavily on understanding moment of inertia.
-
Robotics: Robotic arm design heavily relies on precise calculations of moment of inertia to achieve accurate and efficient movements. The distribution of mass within the arm significantly impacts its ability to maneuver.
-
Aerospace Engineering: Aircraft and spacecraft design involves extensive calculations of moment of inertia to determine stability and maneuverability.
-
Physics Research: Moment of inertia plays a key role in various physics research areas, such as studying the rotation of celestial bodies and the dynamics of molecules.
Beyond the Basics: Radius of Gyration
The radius of gyration (k) is a related concept that provides a measure of how far from the axis of rotation the mass of a body is effectively concentrated. It's defined as:
k = √(I/M)
Where:
kis the radius of gyrationIis the moment of inertiaMis the mass
The radius of gyration simplifies calculations and provides a more intuitive understanding of mass distribution in relation to rotation. It has the same units as distance (meters).
Conclusion: Mastering Moment of Inertia and its Unit
The kilogram-meter squared (kg⋅m²) is the fundamental unit for expressing moment of inertia, reflecting the interplay between mass and distance from the axis of rotation. Understanding this unit is essential for accurately calculating rotational motion and tackling various applications across physics and engineering. From calculating the spin of a simple cylinder to designing complex aerospace systems, the moment of inertia and its unit form the bedrock of rotational dynamics. Mastering its calculation and application opens doors to a deeper understanding of the world around us and empowers you to tackle a wide range of challenging problems. Through a thorough understanding of the concepts and practical examples presented, you are now better equipped to confidently handle problems involving moment of inertia and its significant role in rotational mechanics. Remember to always use the appropriate formulas for various shapes and utilize the parallel axis theorem for simplifying calculations when necessary.
Latest Posts
Latest Posts
-
Which Is True Regarding Ionic Compounds
Apr 11, 2025
-
Which Is The Largest Satellite Of Solar System
Apr 11, 2025
-
Is Blood A Type Of Epithelial Tissue
Apr 11, 2025
-
10 6 Rounded To The Nearest Tenth
Apr 11, 2025
-
The Amount Of Water Vapor Present In Air
Apr 11, 2025
Related Post
Thank you for visiting our website which covers about Si Unit For Moment Of Inertia . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.