Quotient Of A Number And 3
News Leon
Apr 06, 2025 · 5 min read
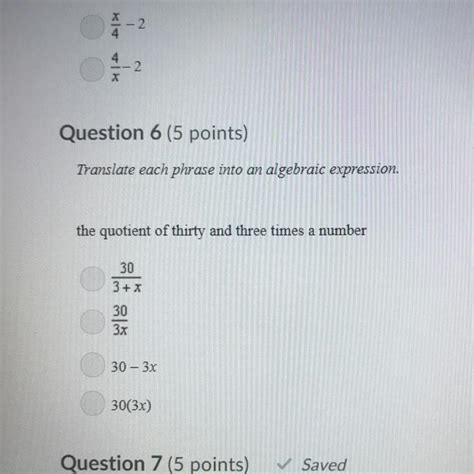
Table of Contents
Quotient of a Number and 3: A Deep Dive into Division and its Applications
The seemingly simple concept of finding the quotient of a number and 3 opens a fascinating gateway into the world of mathematics, encompassing various theoretical and practical applications. This exploration delves into the core principles of division, its representation, its relevance in diverse fields, and the intriguing patterns and properties that emerge when we repeatedly divide a number by 3.
Understanding Division and Quotients
Division, fundamentally, is the inverse operation of multiplication. While multiplication involves combining equal groups, division separates a quantity into equal parts. When we divide a number by 3, we're essentially determining how many groups of 3 can be formed from that number. The result of this division is called the quotient. The number being divided is the dividend, and the number we're dividing by (in this case, 3) is the divisor. Any remaining amount that can't be divided evenly into groups of 3 is called the remainder.
For example, if we divide 10 by 3:
10 ÷ 3 = 3 with a remainder of 1
Here, 10 is the dividend, 3 is the divisor, 3 is the quotient, and 1 is the remainder. This can be expressed as:
Dividend = (Quotient × Divisor) + Remainder
10 = (3 × 3) + 1
This fundamental relationship forms the bedrock of our understanding of division and its applications.
Exploring the Quotient of a Number and 3: Patterns and Properties
Let's examine the quotients obtained when dividing various numbers by 3. Notice that the remainders always fall into a specific pattern: 0, 1, or 2. This is because any number can be expressed in the form 3k, 3k + 1, or 3k + 2, where 'k' is an integer.
-
Numbers Divisible by 3 (Remainder 0): These numbers are multiples of 3 (3, 6, 9, 12, 15, and so on). Their quotients when divided by 3 are whole numbers without any remainder. This divisibility rule is a cornerstone of number theory and finds applications in various mathematical operations.
-
Numbers with Remainder 1: These numbers, when divided by 3, leave a remainder of 1 (1, 4, 7, 10, 13, etc.). Their quotients are whole numbers, but the process always leaves a remainder. Understanding this pattern helps in simplifying calculations and predicting outcomes.
-
Numbers with Remainder 2: Similar to the previous category, these numbers (2, 5, 8, 11, 14, etc.) leave a remainder of 2 when divided by 3. Their quotients are whole numbers, but the remainder consistently indicates a 'shortfall' of one unit to complete a group of 3.
Applications of Division by 3 Across Diverse Fields
The concept of finding the quotient of a number and 3 extends far beyond basic arithmetic. Its applications permeate various disciplines:
1. Computer Science and Algorithms:
-
Hashing: Division by 3 (or any prime number) is often used in hashing algorithms to map data to indices in hash tables. The remainder helps distribute data evenly, minimizing collisions and optimizing data retrieval.
-
Modular Arithmetic: In cryptography and computer security, the modulo operation (finding the remainder after division) plays a crucial role. Modular arithmetic based on division by 3 (or other numbers) is fundamental to many encryption techniques.
-
Data Structures: Certain data structures, like ternary trees (trees where each node has at most three children), leverage the concept of division by 3 to organize and access data efficiently.
2. Engineering and Physics:
-
Load Balancing: In engineering, distributing loads evenly among three support structures often involves division by 3. This ensures optimal stress distribution and prevents structural failure.
-
Signal Processing: Division by 3 can be involved in signal processing techniques, such as digital filter design and spectral analysis, especially when dealing with signals with three distinct components or frequencies.
-
Geometry and Measurement: Dividing lengths, areas, or volumes into three equal parts frequently involves this operation.
3. Everyday Life:
-
Sharing and Distribution: Dividing items equally amongst three people is a common scenario that requires calculating the quotient and handling any remainder (e.g., dividing 10 candies amongst 3 children).
-
Measurement Conversions: Converting units sometimes involves division by 3 (e.g., converting feet to yards).
-
Time Management: Dividing a 3-hour task into equal segments for efficient task completion requires the use of division.
Advanced Concepts Related to Division by 3
Exploring the quotient of a number and 3 can lead to more advanced mathematical concepts:
1. Modular Arithmetic and Congruences:
The remainder obtained when a number is divided by 3 is crucial in modular arithmetic. Two numbers are congruent modulo 3 if they have the same remainder when divided by 3. This concept is fundamental in number theory and has applications in cryptography and abstract algebra.
2. Number Theory and Divisibility Rules:
The divisibility rule for 3 (a number is divisible by 3 if the sum of its digits is divisible by 3) is directly related to the concept of quotients and remainders. Understanding this rule facilitates quick mental calculations and problem-solving.
3. Recursion and Iterative Processes:
Repeatedly dividing a number by 3 until reaching a certain condition can be used to create iterative algorithms and recursive functions in computer science. This repetitive process often reveals patterns and properties that might not be immediately apparent.
Conclusion: The Unassuming Power of Division by 3
The seemingly simple operation of dividing a number by 3 unveils a rich tapestry of mathematical concepts and practical applications. From the fundamental principles of division to advanced concepts like modular arithmetic and recursive algorithms, this seemingly straightforward operation underpins numerous fields. By understanding the patterns, properties, and diverse applications of quotients resulting from division by 3, we gain a deeper appreciation of the power and elegance of mathematics in our world. Its pervasiveness underscores the importance of mastering fundamental arithmetic operations and recognizing their significance beyond elementary calculations. The seemingly simple act of division by 3 is a powerful tool with far-reaching implications in the world of mathematics and beyond.
Latest Posts
Latest Posts
-
All Of The Following Are Communicable Diseases Except
Apr 09, 2025
-
Through Which Of The Following Media Can Sound Waves Travel
Apr 09, 2025
-
Study Of Animal Behaviour Is Called
Apr 09, 2025
-
What Is The Final Product Of The Calvin Cycle
Apr 09, 2025
-
Write A Letter For Increment Of Salary
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Quotient Of A Number And 3 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.