Probability Of Sum Of Two Dice
News Leon
Mar 30, 2025 · 5 min read
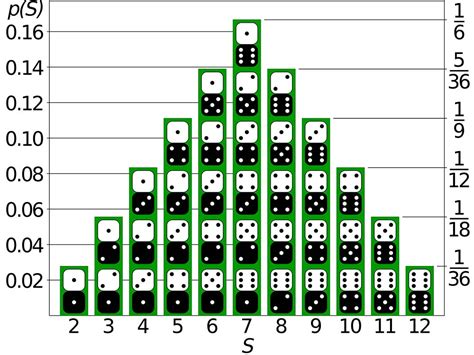
Table of Contents
The Probability of the Sum of Two Dice: A Comprehensive Guide
Rolling two dice is a classic example used to illustrate fundamental concepts in probability. While seemingly simple, understanding the probability distribution of the sum of two dice reveals deeper insights into probability theory and its applications. This comprehensive guide explores this topic in detail, covering everything from basic calculations to advanced considerations.
Understanding Basic Probability
Before diving into the specifics of two dice, let's refresh our understanding of basic probability. Probability is the measure of the likelihood of an event occurring. It's expressed as a number between 0 and 1, where 0 represents impossibility and 1 represents certainty. The probability of an event is calculated as:
Probability (Event) = (Number of Favorable Outcomes) / (Total Number of Possible Outcomes)
For a single six-sided die, the total number of possible outcomes is 6 (1, 2, 3, 4, 5, 6). The probability of rolling any specific number, say a 3, is 1/6.
Calculating the Probability of Sums with Two Dice
When we roll two dice, the number of possible outcomes increases significantly. Each die has six possible outcomes, and since the rolls are independent, we use the multiplication principle. The total number of possible outcomes when rolling two dice is 6 * 6 = 36. These outcomes can be represented as ordered pairs (x, y), where x is the result of the first die and y is the result of the second.
Now, let's consider the probability of obtaining different sums:
Possible Sums and Their Probabilities
The minimum sum is 2 (1 + 1) and the maximum sum is 12 (6 + 6). Let's analyze the probability of each possible sum:
- Sum of 2: Only one combination: (1, 1). Probability = 1/36.
- Sum of 3: Two combinations: (1, 2), (2, 1). Probability = 2/36 = 1/18.
- Sum of 4: Three combinations: (1, 3), (2, 2), (3, 1). Probability = 3/36 = 1/12.
- Sum of 5: Four combinations: (1, 4), (2, 3), (3, 2), (4, 1). Probability = 4/36 = 1/9.
- Sum of 6: Five combinations: (1, 5), (2, 4), (3, 3), (4, 2), (5, 1). Probability = 5/36.
- Sum of 7: Six combinations: (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1). Probability = 6/36 = 1/6.
- Sum of 8: Five combinations: (2, 6), (3, 5), (4, 4), (5, 3), (6, 2). Probability = 5/36.
- Sum of 9: Four combinations: (3, 6), (4, 5), (5, 4), (6, 3). Probability = 4/36 = 1/9.
- Sum of 10: Three combinations: (4, 6), (5, 5), (6, 4). Probability = 3/36 = 1/12.
- Sum of 11: Two combinations: (5, 6), (6, 5). Probability = 2/36 = 1/18.
- Sum of 12: Only one combination: (6, 6). Probability = 1/36.
This data illustrates a symmetrical probability distribution. The probability increases towards the middle (sum of 7) and decreases symmetrically towards the extremes (sums of 2 and 12).
Visualizing the Probability Distribution
A visual representation, such as a bar graph or histogram, can effectively illustrate the probability distribution. The x-axis would represent the possible sums (2 through 12), and the y-axis would represent the probability of each sum. This visualization clearly shows the symmetrical nature of the distribution and the peak probability at a sum of 7.
Expected Value and Variance
In probability theory, the expected value (or mean) represents the average outcome we'd expect over many trials. For the sum of two dice, the expected value is calculated as the sum of each possible sum multiplied by its probability:
E(X) = Σ [x * P(X = x)] where x represents the sum and P(X = x) is its probability.
Calculating this for two dice yields an expected value of 7.
The variance measures the spread or dispersion of the probability distribution. A higher variance indicates a greater spread of possible outcomes. The formula for variance is:
Var(X) = E[(X - μ)²] = Σ [(x - μ)² * P(X = x)] where μ is the expected value.
The variance for the sum of two dice is 35/6. The standard deviation, the square root of the variance, is approximately 2.42.
Applications and Further Considerations
The probability distribution of the sum of two dice has applications beyond simple games of chance. It serves as a fundamental building block for understanding more complex probability models. For instance:
- Simulation and Modeling: The distribution can be used to simulate real-world events with similar probability patterns.
- Statistical Inference: Understanding the distribution is crucial for hypothesis testing and statistical analysis.
- Game Design: Game designers utilize these probabilities to balance gameplay and create fair and engaging experiences.
Beyond Six-Sided Dice
The principles discussed here can be extended to dice with different numbers of sides. The total number of outcomes would change, and consequently, the probability distribution of the sums. For example, with two four-sided dice, the minimum sum would be 2 and the maximum 8, with a different probability distribution than the six-sided case.
Conditional Probability
We can also explore conditional probability. For example, what is the probability of rolling a sum of 8 given that the first die shows a 3? This changes the sample space, and the calculation becomes significantly simpler.
Independent vs. Dependent Events
This discussion assumes the dice rolls are independent events (the outcome of one roll doesn't affect the other). If the dice were somehow linked, making the events dependent, the probability calculations would be significantly more complex and require a different approach, likely involving conditional probabilities.
Conclusion
Understanding the probability distribution of the sum of two dice is a cornerstone of probability theory. From calculating basic probabilities to visualizing the distribution and exploring concepts like expected value and variance, this seemingly simple problem offers rich insights into the fundamentals of probability and its wide-ranging applications. By mastering these concepts, you build a solid foundation for tackling more advanced probability problems and real-world scenarios. Remember that visualizing the probability distribution and understanding its symmetry are key to grasping the full picture. The more you practice with these calculations and visualizations, the more intuitive these probabilistic concepts will become.
Latest Posts
Latest Posts
-
During Glycolysis Glucose Is Broken Down Into What 3 Carbon Compound
Apr 01, 2025
-
Is Digesting Food A Physical Or Chemical Change
Apr 01, 2025
-
A Free Negative Charge Released In An Electric Field Will
Apr 01, 2025
-
How Many Chromosomes In A Human Liver Cell
Apr 01, 2025
-
A Cell With A Diploid Number Of 24 Undergoes Meiosis
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Probability Of Sum Of Two Dice . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
