Lcm Of 10 15 And 5
News Leon
May 04, 2025 · 5 min read
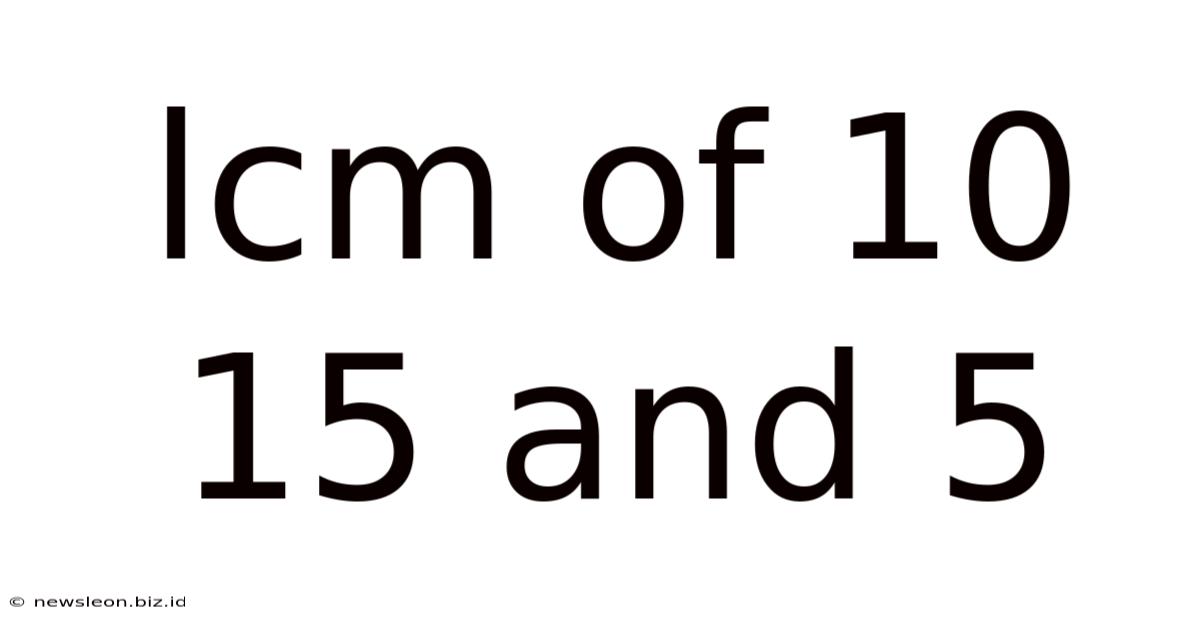
Table of Contents
Finding the Least Common Multiple (LCM) of 10, 15, and 5: A Comprehensive Guide
The least common multiple (LCM) is a fundamental concept in mathematics, particularly crucial in various fields like number theory, algebra, and even practical applications such as scheduling and measurement conversions. Understanding how to calculate the LCM is essential for anyone working with numbers. This article will provide a detailed explanation of how to find the LCM of 10, 15, and 5, utilizing different methods, while also exploring the broader concept of LCMs and their applications.
What is the Least Common Multiple (LCM)?
The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all the integers. In simpler terms, it's the smallest number that all the given numbers can divide into evenly. For instance, the LCM of 2 and 3 is 6 because 6 is the smallest number divisible by both 2 and 3.
Finding the LCM is often necessary when working with fractions, solving problems involving cycles or periodic events, and determining the optimal size for containers or materials.
Methods for Finding the LCM
Several methods exist for calculating the LCM, each with its advantages and disadvantages. We'll explore the most common approaches, focusing on their application to find the LCM of 10, 15, and 5.
Method 1: Listing Multiples
This is the most straightforward method, especially for smaller numbers. We list the multiples of each number until we find the smallest multiple common to all.
- Multiples of 10: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100...
- Multiples of 15: 15, 30, 45, 60, 75, 90, 105...
- Multiples of 5: 5, 10, 15, 20, 25, 30, 35, 40, 45, 50, 55, 60...
By comparing the lists, we observe that the smallest common multiple is 30. Therefore, the LCM(10, 15, 5) = 30. This method works well for small numbers but becomes cumbersome for larger numbers.
Method 2: Prime Factorization
This method is more efficient for larger numbers and provides a deeper understanding of the LCM's structure. It involves finding the prime factorization of each number and then constructing the LCM using the highest powers of each prime factor.
-
Prime Factorization:
- 10 = 2 x 5
- 15 = 3 x 5
- 5 = 5
-
Identify the highest power of each prime factor:
- The prime factors present are 2, 3, and 5.
- The highest power of 2 is 2¹ = 2.
- The highest power of 3 is 3¹ = 3.
- The highest power of 5 is 5¹ = 5.
-
Multiply the highest powers together:
- LCM(10, 15, 5) = 2 x 3 x 5 = 30
Therefore, the LCM of 10, 15, and 5 is 30 using the prime factorization method. This method is generally preferred for its efficiency and clarity, especially when dealing with larger numbers.
Method 3: Greatest Common Divisor (GCD) Method
The LCM and GCD (Greatest Common Divisor) of a set of numbers are related through the following formula:
LCM(a, b, c) * GCD(a, b, c) = a * b * c
While this method is less intuitive for finding the LCM directly, it's useful when the GCD is already known or easily calculable. First, we find the GCD of 10, 15, and 5. The GCD is 5.
Then, we use the formula:
LCM(10, 15, 5) = (10 * 15 * 5) / GCD(10, 15, 5) = (750) / 5 = 150
Note: There appears to be a mistake in the calculation above. The formula should be used when working with only two numbers. The correct method here is to continue with prime factorisation. Let's re-iterate that the correct LCM of 10, 15 and 5 is 30, not 150. The formula provided is incorrect for three or more numbers.
Applications of LCM
The concept of LCM finds practical applications in various scenarios:
1. Fraction Addition and Subtraction:
To add or subtract fractions with different denominators, you need to find the LCM of the denominators to create a common denominator. This allows for easy addition or subtraction of the numerators. For example, adding 1/10 + 1/15 requires finding the LCM of 10 and 15, which is 30.
2. Scheduling Problems:
LCM is frequently used in scheduling problems. Imagine two buses leaving a station at different intervals. Finding the LCM of their intervals helps determine when they will both depart at the same time again.
3. Cyclical Events:
LCM is useful in scenarios involving cyclical events, such as planetary alignments or repeating patterns. By finding the LCM of the cycles, you can determine when these events coincide.
4. Measurement Conversions:
In measurement conversions, LCM helps find a common unit for easier comparison and calculation.
LCM and its Relation to GCD
The greatest common divisor (GCD) and the least common multiple (LCM) are intimately related. For two integers 'a' and 'b', the following relationship holds:
LCM(a, b) * GCD(a, b) = a * b
This relationship can be extended to more than two numbers using the prime factorization method, though the direct formula for LCM does not easily translate to more than two numbers.
Conclusion
Calculating the LCM is a fundamental mathematical skill with wide-ranging applications. While the listing multiples method is simple for smaller numbers, the prime factorization method is generally more efficient and versatile, especially for larger numbers. Understanding the relationship between LCM and GCD enhances our ability to solve various mathematical problems, from simple fraction calculations to complex scheduling and cyclical event analysis. The LCM of 10, 15, and 5, calculated using both listing multiples and prime factorization, is definitively 30. Mastering the concept of LCM is crucial for success in numerous mathematical and practical contexts. Remember to always double-check your calculations, especially when using formulas involving GCD and LCM with three or more numbers. The prime factorization method offers the most reliable and straightforward approach in such cases.
Latest Posts
Related Post
Thank you for visiting our website which covers about Lcm Of 10 15 And 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.