Is Work A Scalar Or Vector Quantity
News Leon
Apr 03, 2025 · 6 min read
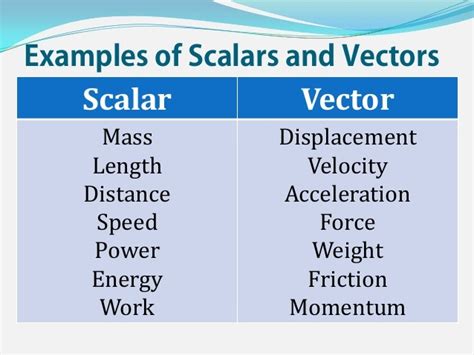
Table of Contents
Is Work a Scalar or Vector Quantity? A Comprehensive Exploration
The question of whether work is a scalar or vector quantity often arises in physics discussions. While seemingly straightforward, a complete understanding requires delving into the fundamental definitions of work, scalar quantities, and vector quantities, as well as exploring related concepts like energy and power. This comprehensive article will dissect the issue, providing a nuanced and detailed answer.
Understanding Scalar and Vector Quantities
Before tackling the core question, let's establish a clear understanding of scalar and vector quantities. This foundational knowledge is crucial for grasping the nature of work.
Scalar Quantities
A scalar quantity is a quantity that is fully described by its magnitude alone. It has only size or amount, with no associated direction. Examples of scalar quantities include:
- Mass: The amount of matter in an object.
- Temperature: A measure of hotness or coldness.
- Speed: The rate at which an object covers distance.
- Energy: The capacity to do work.
- Time: The duration of an event.
These quantities can be added, subtracted, and multiplied using simple arithmetic.
Vector Quantities
A vector quantity, in contrast, requires both magnitude and direction for its complete description. It has both size and a specific orientation in space. Examples of vector quantities include:
- Displacement: The change in position of an object.
- Velocity: The rate of change of displacement.
- Acceleration: The rate of change of velocity.
- Force: A push or pull acting on an object.
- Momentum: The product of mass and velocity.
Vector quantities necessitate more complex mathematical operations, often involving vector addition, subtraction, and scalar multiplication. They are typically represented graphically using arrows, where the length of the arrow denotes the magnitude and the arrowhead indicates the direction.
Defining Work in Physics
Work, in the context of physics, is defined as the energy transferred to or from an object via the application of force along a displacement. This definition is crucial to understanding its scalar nature. The formula for work is:
W = Fd cos θ
Where:
- W represents work.
- F represents the magnitude of the force applied.
- d represents the magnitude of the displacement.
- θ represents the angle between the force vector and the displacement vector.
This equation highlights several key aspects:
- Magnitude of Force and Displacement: Both force and displacement are vector quantities, having both magnitude and direction. However, in the work equation, we use only their magnitudes (F and d).
- Cosine of the Angle: The cosine of the angle (θ) between the force and displacement vectors accounts for the directional component. When the force is applied in the same direction as the displacement (θ = 0°), cos θ = 1, and the work done is maximized. When the force is perpendicular to the displacement (θ = 90°), cos θ = 0, and no work is done. If the force acts in the opposite direction to the displacement (θ = 180°), cos θ = -1, and negative work is done. This negative work indicates energy is being transferred from the object.
Why Work is Considered a Scalar Quantity
Despite being derived from vector quantities (force and displacement), work itself is considered a scalar quantity. This is because the equation includes only the magnitudes of the force and displacement and the cosine of the angle between them, resulting in a single numerical value representing the energy transferred. The direction of the energy transfer is implicitly conveyed by the positive or negative sign of the work done, but no specific spatial direction is associated with the work itself.
Think of lifting a box: you apply an upward force (vector), and the box moves upward (vector). The work done is positive, indicating an energy transfer to the box, but the work itself doesn't have a direction like "upward" or "downward." It’s simply a measure of the energy transferred.
Work and Energy: A Close Relationship
The scalar nature of work is intimately linked to its relationship with energy. Work is essentially a measure of energy transfer. Energy, as mentioned earlier, is a scalar quantity. When work is done on an object, its energy changes. This change can manifest in various forms, such as kinetic energy (energy of motion) or potential energy (stored energy). Both kinetic and potential energy are scalar quantities.
Addressing Potential Misconceptions
Some might argue that since force and displacement are vectors, the work done should also be a vector. However, the crucial point is that the work equation only considers the components of the force vector that are parallel to the displacement vector. The perpendicular component of the force doesn’t contribute to the work done. The result is a scalar quantity representing the net energy transfer.
Another misconception arises from considering the effect of work. While work can cause changes in vector quantities like velocity and momentum, the work itself remains a scalar. The work simply quantifies the energy transfer underlying these changes.
Practical Applications and Examples
The scalar nature of work has significant implications in various fields. Understanding that work is a scalar is essential for calculating energy changes in numerous physical scenarios.
Example 1: Lifting a Weight
Lifting a weight vertically involves doing positive work against gravity. The work done is the product of the weight (force) and the height (displacement). The work itself is a scalar; it's a measure of the energy gained by the weight, irrespective of the direction of lift.
Example 2: Pushing a Box Across a Floor
Pushing a box across a horizontal floor involves work done against friction. The work done is dependent on the force applied parallel to the floor and the distance the box is moved. The resultant work is a scalar value representing the energy expended in overcoming friction.
Example 3: Stretching a Spring
Stretching a spring involves doing positive work, storing potential energy in the spring. This work is a scalar quantity representing the energy stored in the elastic deformation.
Example 4: Braking a Car
Applying brakes to a car involves doing negative work. The friction between the brakes and the wheels reduces the kinetic energy of the car. The work done is negative, representing the energy transferred from the car to the surroundings as heat.
Conclusion: Work – A Scalar Quantity in Physics
In conclusion, while work is calculated using vector quantities (force and displacement), it is itself a scalar quantity. It represents the energy transferred to or from an object, a quantity that is characterized solely by its magnitude (with a positive or negative sign to denote the direction of energy transfer). The directional aspects of force and displacement are incorporated through the cosine term in the work equation, resulting in a single numerical value that quantifies the energy exchange. This fundamental understanding is crucial for various applications in physics and engineering. Failing to recognize the scalar nature of work can lead to misunderstandings and errors in calculations and analyses of energy transfer in physical systems. The distinction between scalar and vector quantities is a cornerstone of physics, and the case of work provides a compelling example of this distinction in action.
Latest Posts
Latest Posts
-
What Is The Prime Factorization Of 120
Apr 04, 2025
-
Do Nonmetals Gain Or Lose Electrons
Apr 04, 2025
-
Oxygen Released During Photosynthesis Comes From
Apr 04, 2025
-
Which Of The Following Defines A Coenzyme
Apr 04, 2025
-
When There Is A Decrease In Both Demand And Supply
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Is Work A Scalar Or Vector Quantity . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
