Is Friction A Non Conservative Force
News Leon
Apr 03, 2025 · 6 min read
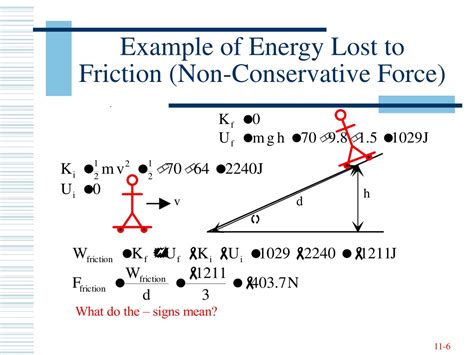
Table of Contents
- Is Friction A Non Conservative Force
- Table of Contents
- Is Friction a Non-Conservative Force? A Deep Dive into Energy and Work
- Understanding Conservative Forces
- The Nature of Friction: Why It's Non-Conservative
- Mathematical Representation and Examples
- Contrasting Friction with Conservative Forces: A Comparative Analysis
- Implications of Friction's Non-Conservative Nature
- Conclusion: Friction's Irreversible Energy Transformation
- Latest Posts
- Latest Posts
- Related Post
Is Friction a Non-Conservative Force? A Deep Dive into Energy and Work
Friction, a ubiquitous force in our everyday lives, often presents a puzzling question in physics: is friction a conservative or non-conservative force? The answer, simply put, is non-conservative. Understanding why requires a deep dive into the concepts of conservative forces, potential energy, and the nature of frictional interactions. This comprehensive article will explore this topic thoroughly, examining the characteristics of friction and contrasting it with the behavior of conservative forces. We'll delve into real-world examples and explore the implications of friction's non-conservative nature on various physical systems.
Understanding Conservative Forces
Before tackling friction, let's establish a clear understanding of what constitutes a conservative force. A conservative force is one for which the work done in moving an object between two points is independent of the path taken. This means the work done only depends on the object's initial and final positions, not the route it followed. Crucially, a conservative force is associated with a potential energy function. The change in potential energy equals the negative of the work done by the conservative force.
Some key characteristics of conservative forces include:
- Path independence: The work done is independent of the path taken.
- Potential energy function: A potential energy function exists, representing the stored energy related to the force.
- Closed-path work: The work done by a conservative force around a closed path is always zero.
Examples of conservative forces include:
- Gravity: The work done by gravity on an object moving between two points depends only on the change in height, not the path taken.
- Electrostatic force: The work done by an electrostatic force on a charged particle depends only on the initial and final positions of the particle relative to the charge source.
- Elastic spring force: The work done by a spring depends only on the initial and final extension or compression of the spring.
The Nature of Friction: Why It's Non-Conservative
Unlike conservative forces, friction is a non-conservative force. This means the work done by friction depends heavily on the path taken. Let's examine why:
-
Path dependence: Imagine sliding a block across a rough surface. The work done by friction will be greater if the block travels a longer distance. The path taken directly affects the total energy dissipated by friction. A longer path means more contact with the rough surface, resulting in more energy lost as heat.
-
Energy dissipation: Friction converts mechanical energy into other forms of energy, primarily heat. This energy transformation is irreversible; the heat generated cannot spontaneously be converted back into mechanical energy to restore the block's initial state. This inherent irreversibility is a hallmark of non-conservative forces. In contrast, conservative forces are associated with energy storage that can be fully recovered.
-
No potential energy function: A potential energy function cannot be defined for frictional forces. The energy lost due to friction isn't stored in a way that can be readily retrieved. It's dissipated into the environment as thermal energy, increasing the system's internal energy but not its potential energy in the context of the force itself.
Mathematical Representation and Examples
The work done by friction can be mathematically represented as:
W<sub>friction</sub> = -μ<sub>k</sub> * N * d
Where:
- W<sub>friction</sub> is the work done by kinetic friction.
- μ<sub>k</sub> is the coefficient of kinetic friction.
- N is the normal force.
- d is the distance over which the object slides.
Notice the negative sign. This indicates that the work done by friction is always negative in the direction of motion. It opposes the motion and reduces the kinetic energy of the system.
Let's illustrate this with some examples:
Example 1: Sliding a block on a rough surface: If you slide a block across a table, the frictional force opposes the motion and converts some of the block's kinetic energy into heat. The work done by friction depends on the distance the block slides. Sliding it a longer distance results in more work done by friction and greater energy loss.
Example 2: Rolling a ball on a rough surface: Even when rolling, friction plays a significant role, though the type of friction is different (rolling friction). A rolling ball eventually comes to a stop due to frictional losses. The distance the ball travels determines the amount of energy dissipated as heat.
Example 3: Air resistance: Air resistance, another form of friction, depends on factors such as the speed of the object and the density of the air. The faster the object moves, the greater the air resistance, and the more energy is lost as heat. A skydiver's terminal velocity is a result of the balance between gravity (a conservative force) and air resistance (a non-conservative force).
Contrasting Friction with Conservative Forces: A Comparative Analysis
The table below summarizes the key differences between friction (a non-conservative force) and a typical conservative force like gravity:
| Feature | Friction (Non-Conservative) | Gravity (Conservative) |
|---|---|---|
| Path Dependence | Work depends on the path taken | Work independent of the path taken |
| Energy Conversion | Converts mechanical energy into heat | Converts potential energy to kinetic and vice versa |
| Potential Energy | No associated potential energy function | Associated with a potential energy function (mgh) |
| Closed-path Work | Work done around a closed path is not zero | Work done around a closed path is zero |
| Reversibility | Energy conversion is irreversible | Energy conversion is reversible (ideally) |
| Direction | Always opposes motion | Depends on the configuration of the masses involved |
Implications of Friction's Non-Conservative Nature
The non-conservative nature of friction has significant implications in various areas of physics and engineering:
-
Energy efficiency: In machines and engines, friction leads to energy losses as heat, reducing efficiency. Engineers strive to minimize friction through lubrication and improved designs to maximize the useful work output.
-
Thermal effects: The heat generated by friction can be beneficial in some applications (brakes), but it can also be detrimental in others (increased wear and tear on moving parts).
-
System modeling: Modeling systems involving friction often requires more complex mathematical techniques compared to systems dominated by conservative forces because the path taken must be explicitly considered.
-
Material science: The study of friction and its effects is crucial for material scientists, who seek to develop materials with reduced friction coefficients for improved performance and durability.
Conclusion: Friction's Irreversible Energy Transformation
In conclusion, friction is definitively a non-conservative force. Its path dependence, energy dissipation as heat, and lack of an associated potential energy function clearly distinguish it from conservative forces. Understanding the non-conservative nature of friction is essential for analyzing and predicting the behavior of various physical systems, designing efficient machines, and developing advanced materials. The irreversible transformation of mechanical energy into heat due to friction is a fundamental aspect of our physical world, impacting everything from the motion of celestial bodies to the operation of everyday devices.
Latest Posts
Latest Posts
-
Every Parallelogram Is A Rhombus True Or False
Apr 06, 2025
-
Is Water More Polar Than Ethanol
Apr 06, 2025
-
State Whether The Statement Is True Or False
Apr 06, 2025
-
Eukaryotic Cells May Contain All Of The Following Except
Apr 06, 2025
-
An Infinitely Long Straight Cylindrical Wire
Apr 06, 2025
Related Post
Thank you for visiting our website which covers about Is Friction A Non Conservative Force . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
